
分析 (1)设z=a+bi,(a,b∈R),由|z|=$\sqrt{2}$,z的虚部为1,求出a,b;
(2)化简m2+m+mz2,利用m2+m+mz2是纯虚数得到关于m的式子解之.
解答 解:(1)设z=a+bi,(a,b∈R),…(1分)
则a2+b2=2,b=1…(2分)
因为在复平面内表示的点位于第二象限,所以a>0,
所以a=1,b=1,
所以z=-1+i…(6分)
(2)由(1)得z=-1+i
∴z2=(-1+i)2=-2i…(7分)
∴m2+m+mz2=m2+m-2mi…(8分)
又∵m2+m+mz2是纯虚数
∴$\left\{\begin{array}{l}{m^2}+m=0\\-2m≠0\end{array}\right.$…(11分)
∴m=-1…(12分)
点评 本题考查了复数的模、基本概念;关键是由题意得到关于a,b 的方程求出复数z;复数a+bi为纯虚数,其实部为0,虚部不为0,.


科目:高中数学 来源: 题型:选择题
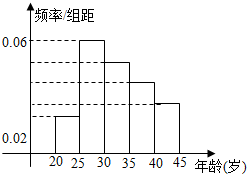 某居民小区年龄在20岁到45岁的居民共有150人,如图是他们上网情况的频率分布直方图,现已知年龄在[30,35),[40,45]的人数分别是39、21人,则年龄在[35,40)的频数( )
某居民小区年龄在20岁到45岁的居民共有150人,如图是他们上网情况的频率分布直方图,现已知年龄在[30,35),[40,45]的人数分别是39、21人,则年龄在[35,40)的频数( )| A. | 6 | B. | 9 | C. | 30 | D. | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
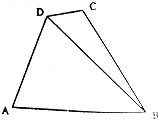 随州市某处有如图所示的A、B、C、D四个景点,目前AD、AB、DC之间已修建公路,市政府为了更好发展随州的旅游产业,决定新修建两条公路用以连接B、D两景点和B、C两景点.现测得AD=5km,AB=7km,∠ADB=60°,∠ADC=105°,∠CBD=15°
随州市某处有如图所示的A、B、C、D四个景点,目前AD、AB、DC之间已修建公路,市政府为了更好发展随州的旅游产业,决定新修建两条公路用以连接B、D两景点和B、C两景点.现测得AD=5km,AB=7km,∠ADB=60°,∠ADC=105°,∠CBD=15°查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,0) | B. | (2,1) | C. | (0,-1) | D. | $({\frac{3}{2},\frac{1}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$ | B. | $\overrightarrow{DA}$ | C. | $\overrightarrow{BC}$ | D. | $\overrightarrow{0}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在一次数学竞赛中,高一•1班30名学生的成绩茎叶图如图所示:若将学生按成绩由低到高编为1-30号,再用系统抽样的方法从中抽取6人,则其中成绩在区间[73,90]上的学生人数为( )
在一次数学竞赛中,高一•1班30名学生的成绩茎叶图如图所示:若将学生按成绩由低到高编为1-30号,再用系统抽样的方法从中抽取6人,则其中成绩在区间[73,90]上的学生人数为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com