
分析 (1)利用数列的递推关系式求出首项,判断数列是等比数列,然后求解通项公式.
(2)利用${b_n}={log_{\frac{1}{3}}}{a_n}$,化简数列{anbn}通项公式,然后利用错位相减法求和,推出结果即可.
解答 (本小题满分10分)
解:(1)当n=1时,由2S1=1-a1得:${a_1}=\frac{1}{3}$.2Sn=1-an(n∈N*).
可得2Sn-1=1-an-1(n∈N*).
两式相减可得:an=$\frac{1}{3}$an-1 n≥2,
∴数列{an}是等比数列,首项为$\frac{1}{3}$,公比为$\frac{1}{3}$,
∴an=$\frac{1}{{3}^{n}}$;
(2)证明:∵${a_n}=\frac{1}{3^n}$(n∈N*),∴${b_n}={log_{\frac{1}{3}}}{a_n}={log_{\frac{1}{3}}}{({\frac{1}{3}})^n}=n$.
∴${a_n}{b_n}=\frac{n}{3^n}$∴${T_n}=\frac{1}{3}+\frac{2}{3^2}+\frac{3}{3^3}+…+\frac{n}{3^n}$;
∴$\frac{1}{3}{T_n}=\frac{1}{3^2}+\frac{2}{3^3}+…+\frac{n-1}{3^n}+\frac{n}{{{3^{n+1}}}}$
∴$\frac{2}{3}{T_n}=\frac{1}{3}+({\frac{1}{3^2}+\frac{1}{3^3}+…+\frac{1}{3^n}})-\frac{n}{{{3^{n+1}}}}=\frac{{\frac{1}{3}({1-\frac{1}{3^n}})}}{{1-\frac{1}{3}}}-\frac{n}{{{3^{n+1}}}}=\frac{1}{2}-\frac{2n+3}{{2×{3^{n+1}}}}$
∴${T_n}=\frac{3}{4}-\frac{2n+3}{{4×{3^n}}}<\frac{3}{4}$.
点评 本题考查数列的递推关系式的应用,数列求和,考查计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
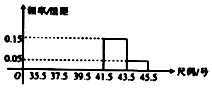 某商场为了了解某日旅游鞋的销售情况,抽取了部分顾客所购鞋的尺寸,将所得数据整理后,画出频率分布直方图如图所示.已知从左到右前3个小组的频率之比为1:2:3,第4小组与第5小组的频率分布如图所示,第2小组的频数为10,则第4小组顾客的人数是( )
某商场为了了解某日旅游鞋的销售情况,抽取了部分顾客所购鞋的尺寸,将所得数据整理后,画出频率分布直方图如图所示.已知从左到右前3个小组的频率之比为1:2:3,第4小组与第5小组的频率分布如图所示,第2小组的频数为10,则第4小组顾客的人数是( )| A. | 15 | B. | 20 | C. | 25 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若命题p为真命题,命题q为假命题,则命题“p∨(¬q)”为真命题 | |
| B. | 命题“若a+b≠7,则a≠2或b≠5”为真命题 | |
| C. | 命题p:?x>0,sinx>2x-1,则¬p为?x>0,sinx≤2x-1 | |
| D. | 命题“若x2-x=0,则x=0或x=1”的否命题为“若x2-x=0,则x≠0且x≠1” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
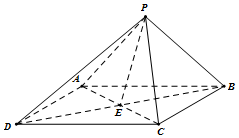 如图,四棱锥P-ABCD的底面ABCD是平行四边形,PA=PB=PC=6,∠APB=∠BPC=∠CPA=90°,AC∩BD=E.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,PA=PB=PC=6,∠APB=∠BPC=∠CPA=90°,AC∩BD=E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com