
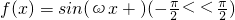 ,以下列四个命题中的两个为条件,余下的两个为结论,写出你认为正确的一个命题________.(序号表示)
,以下列四个命题中的两个为条件,余下的两个为结论,写出你认为正确的一个命题________.(序号表示) 对称;
对称;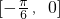 上是增函数;
上是增函数; 对称;
对称; 对称故2×
对称故2× +φ=
+φ= 或2×
或2× +φ=-
+φ=- ,故φ=
,故φ= 或φ=
或φ=
 <φ<
<φ< ∴φ=
∴φ= ,即函数表达式为y=sin(2x+
,即函数表达式为y=sin(2x+ )可以证得②③是这个函数的特性.故①④?②③
)可以证得②③是这个函数的特性.故①④?②③ 对称,可得2×
对称,可得2× +φ=0或π故可以解得φ=
+φ=0或π故可以解得φ= 或φ=
或φ= ,同理可以得到函数的解析式为y=sin(2x+
,同理可以得到函数的解析式为y=sin(2x+ ),可以证得①②是这个函数的特性.故③④?①②
),可以证得①②是这个函数的特性.故③④?①②

科目:高中数学 来源:山东省梁山一中2010-2011学年高一下学期期末考试数学试题 题型:022
对于函数![]() 给出下列四个命题:
给出下列四个命题:
①该函数是以π为最小正周期的周期函数;
②当且仅当x=π+kπ(k∈Z)时,该函数取得最小值是-1;
③该函数图象关于![]() 对称;
对称;
④当且仅当![]()
其中正确命题的序号是________(请将所有正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
①该函数的值域为[-1,1] ②当且仅当x=2kπ+![]() (k∈Z)时,该函数取得最大值1 ③该函数是以π为最小正周期的周期函数 ④当且仅当2kπ+π<x<2kπ+
(k∈Z)时,该函数取得最大值1 ③该函数是以π为最小正周期的周期函数 ④当且仅当2kπ+π<x<2kπ+![]() (k∈Z)时,f(x)<0
(k∈Z)时,f(x)<0
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2013届辽宁省辽南协作体高一下学期期中考试数学(理) 题型:填空题
对于函数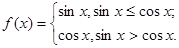 给出下列四个命题:
给出下列四个命题:
①该函数是以π为最小正周期的周期函数;
②当且仅当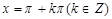 时,该函数取得最小值是-1;
时,该函数取得最小值是-1;
③该函数图象关于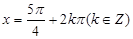 对称;
对称;
④当且仅当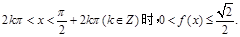
其中正确命题的序号是_____________(请将所有正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源:2013届山东省高一下学期期末考试数学 题型:填空题
对于函数 给出下列四个命题:
给出下列四个命题:
①该函数是以π为最小正周期的周期函数;
②当且仅当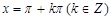 时,该函数取得最小值是-1;
时,该函数取得最小值是-1;
③该函数图象关于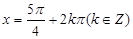 对称;
对称;
④当且仅当
其中正确命题的序号是___________(请将所有正确命题的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com