已知动圆C经过坐标原点O,且圆心C在直线l:2x+y=4上.
(1)求半径最小时的圆C的方程;
(2)求证:动圆C恒过一个异于点O的定点.
【答案】
分析:(1)根据题意可设圆心的坐标为(a,4-2a),又因为动圆C经过坐标原点O,所以动圆的半径r=
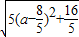
,根据二次函数的性质进而得到圆的方程.
(2)设定点坐标(x
,y
),可得x
2-2ax
+y
2-2(4-2a)y
=0,即a(4y
-2x
)+(x
2+y
2-8y
)=0,利用过定点的知识可得:4y
-2x
=0且x
2+y
2-8y
=0,进而得到定点.
解答:解:(1)因为圆心C在直线l:2x+y=4上,
所以设圆心的坐标为(a,4-2a).
又因为动圆C经过坐标原点O,
所以动圆的半径r=

,所以半径r的最小值为
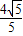
.
并且此时圆的方程为:(x-

)
2-(y-

)
2=
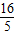
.
(2)设定点坐标(x
,y
),因为圆的方程为:(x-a)
2+[y-(4-2a)]
2=a
2+(4-2a)
2所以x
2-2ax
+y
2-2(4-2a)y
=0,
即a(4y
-2x
)+(x
2+y
2-8y
)=0,
因为当a为变量时,x
,y
却能使该等式恒成立,
所以只可能4y
-2x
=0且x
2+y
2-8y
=0
即解方程组可得:y
=

,x
=
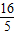
或者y
=0,x
=0(舍去)
所以圆C恒过一定点(

,

).
点评:解决此类问题的关键是熟练掌握圆的标准方程,以及直线或者圆过定点的有关知识.

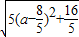 ,根据二次函数的性质进而得到圆的方程.
,根据二次函数的性质进而得到圆的方程. ,所以半径r的最小值为
,所以半径r的最小值为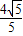 .
. )2-(y-
)2-(y- )2=
)2=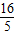 .
. ,x=
,x=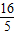 或者y=0,x=0(舍去)
或者y=0,x=0(舍去) ,
, ).
).
