
已知点A(-1,O),B(1,0),动点M的轨迹曲线C满足∠AMB=2![]() ,|
,|![]() |·|
|·|![]() |cos2
|cos2![]() =3
=3
(Ⅰ)求曲线C的方程;
(Ⅱ)试探究曲线C上是否存在点P,使直线PA与PB的斜率kPA·kPB=1?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AM |
| BM |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省实验中学高三(下)第一次综合测试数学试卷(文科)(解析版) 题型:解答题
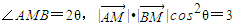 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com