
【题目】设|θ|< ![]() ,n为正整数,数列{an}的通项公式an=sin
,n为正整数,数列{an}的通项公式an=sin ![]() tannθ,其前n项和为Sn
tannθ,其前n项和为Sn
(1)求证:当n为偶函数时,an=0;当n为奇函数时,an=(﹣1) ![]() tannθ;
tannθ;
(2)求证:对任何正整数n,S2n= ![]() sin2θ[1+(﹣1)n+1tan2nθ].
sin2θ[1+(﹣1)n+1tan2nθ].
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】如图,在斜三梭柱ABC﹣A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是棱AB上一点,且OE∥平面BCC1B1
(1)求证:E是AB中点;
(2)若AC1⊥A1B,求证:AC1⊥BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学调查了某班全部 45 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 5 |
未参加书法社团 | 2 | 30 |
(1)从该班随机选 1 名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的 8 名同学中,有 5 名男同学![]() ,3名女同学
,3名女同学![]() .现从这 5 名男同学和 3 名女同学中各随机选 1 人,求
.现从这 5 名男同学和 3 名女同学中各随机选 1 人,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O1和圆O2的极坐标方程分别为ρ=2, ![]() .
.
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程;
(2)求经过两圆交点的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
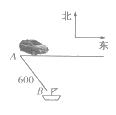
【题目】如图所示,一辆汽车从![]() 市出发沿海岸一条直公路以
市出发沿海岸一条直公路以![]() 的速度向东匀速行驶,汽车开动时,在
的速度向东匀速行驶,汽车开动时,在![]() 市南偏东30°方向距
市南偏东30°方向距![]() 市
市![]() 的海上
的海上![]() 处有一快艇与汽车同时出发,要把一份稿件送给这辆汽车的司机.问快艇至少以多大的速度,以什么样的航向行驶才能最快把稿件送到司机手中?
处有一快艇与汽车同时出发,要把一份稿件送给这辆汽车的司机.问快艇至少以多大的速度,以什么样的航向行驶才能最快把稿件送到司机手中?
查看答案和解析>>
科目:高中数学 来源: 题型:
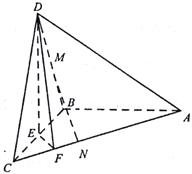
【题目】如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC
(1)求三棱锥D-ABC的体积
(2)求证:平面DAC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN=![]() CA,求证:MN∥平面DEF
CA,求证:MN∥平面DEF
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市有一条东西走向的公路l,现欲经过公路l上的O处铺设一条南北走向的公路m,在施工过程中发现O处的正北方向1百米的A处有一汉代古迹,为了保护古迹,该市委决定以A为圆心,1百米为半径设立一个圆形保护区,为了连通公路l,m,欲再新建一条公路PQ,点P,Q分别在公路l,m上(点P,Q分别在点O的正东、正北方向),且要求PQ与圆A相切.

(1)当点P距O处2百米时,求OQ的长;
(2)当公路PQ的长最短时,求OQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C: ![]() ,点
,点![]() 在x轴的正半轴上,过点M的直线
在x轴的正半轴上,过点M的直线![]() 与抛物线C相交于A,B两点,O为坐标原点.
与抛物线C相交于A,B两点,O为坐标原点.
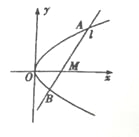
(1)若![]() ,且直线
,且直线![]() 的斜率为1,求以AB为直径的圆的方程;
的斜率为1,求以AB为直径的圆的方程;
(2)是否存在定点M,使得不论直线![]() 绕点M如何转动,
绕点M如何转动, ![]() 恒为定值?
恒为定值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com