
【题目】已知函数f(x)=lg(x2﹣5x+6)和![]() 的定义域分别是集合A、B,
的定义域分别是集合A、B,
(1)求集合A,B;
(2)求集合A∪B,A∩B.
【答案】解:(1)由x2﹣5x+6>0,即(x﹣2)(x﹣3)>0,
解得:x>3或x<2,即A={x|x>3或x<2},
由![]() ,得到
,得到![]() ﹣1≥0,
﹣1≥0,
当x>0时,整理得:4﹣x≥0,即x≤4;
当x<0时,整理得:4﹣x≤0,无解,
综上,不等式的解集为0<x≤4,即B={x|0<x≤4};
(2)∵A={x|x>3或x<2},B={x|0<x≤4},
∴A∪B=R,A∩B={x|0<x<2或3<x≤4}.
【解析】(1)求出f(x)与g(x)的定义域分别确定出A与B即可;
(2)根据A与B,找出A与B的并集,交集即可.
【考点精析】通过灵活运用集合的交集运算,掌握交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立即可以解答此题.
B,反之也成立即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列4个命题,其中正确的命题序号为( )
①|x+ ![]() |的最小值是2 ②
|的最小值是2 ② ![]() 的最小值是2 ③log2x+logx2的最小值是2 ④3x+3﹣x的最小值是2.
的最小值是2 ③log2x+logx2的最小值是2 ④3x+3﹣x的最小值是2.
A.①②③
B.①②④
C.②③④
D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一个正方体的展开图,如果将它还原为正方体,那么NC、DE、AF、BM这四条线段所在的直线是异面直线的有多少对?试以其中一对为例进行证明.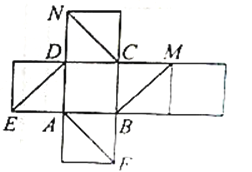
查看答案和解析>>
科目:高中数学 来源: 题型:
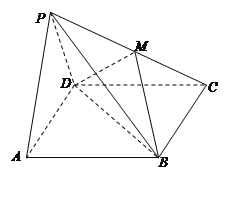
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,面
是矩形,面![]() 底面
底面![]() ,且
,且![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() ,
, ![]() 在
在![]() 上,且
上,且![]() ∥面BDM.
∥面BDM.
(1)求直线PC与平面BDM所成角的正弦值;
(2)求平面BDM与平面PAD所成锐二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来随着我国在教育科研上的投入不断加大,科学技术得到迅猛发展,国内企业的国际竞争力得到大幅提升.伴随着国内市场增速放缓,国内有实力企业纷纷进行海外布局,第二轮企业出海潮到来.如在智能手机行业,国产品牌已在赶超国外巨头,某品牌手机公司一直默默拓展海外市场,在海外共设![]() 多个分支机构,需要国内公司外派大量
多个分支机构,需要国内公司外派大量![]() 后、
后、![]() 后中青年员工.该企业为了解这两个年龄层员工是否愿意被外派工作的态度,按分层抽样的方式从
后中青年员工.该企业为了解这两个年龄层员工是否愿意被外派工作的态度,按分层抽样的方式从![]() 后和
后和![]() 后的员工中随机调查了
后的员工中随机调查了![]() 位,得到数据如下表:
位,得到数据如下表:
愿意被外派 | 不愿意被外派 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(Ⅰ)根据调查的数据,是否有![]() 以上的把握认为“是否愿意被外派与年龄有关”,并说明理由;
以上的把握认为“是否愿意被外派与年龄有关”,并说明理由;
(Ⅱ)该公司举行参观驻海外分支机构的交流体验活动,拟安排![]() 名参与调查的
名参与调查的![]() 后、
后、![]() 后员工参加.
后员工参加.![]() 后员工中有愿意被外派的
后员工中有愿意被外派的![]() 人和不愿意被外派的
人和不愿意被外派的![]() 人报名参加,从中随机选出
人报名参加,从中随机选出![]() 人,记选到愿意被外派的人数为
人,记选到愿意被外派的人数为![]() ;
;![]() 后员工中有愿意被外派的
后员工中有愿意被外派的![]() 人和不愿意被外派的
人和不愿意被外派的![]() 人报名参加,从中随机选出
人报名参加,从中随机选出![]() 人,记选到愿意被外派的人数为
人,记选到愿意被外派的人数为![]() ,求
,求![]() 的概率.
的概率.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式:![]() ,其中
,其中![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
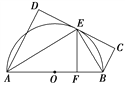
【题目】如图所示,AB为⊙O的直径,直线CD与⊙O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.
证明:(1)∠FEB=∠CEB;
(2)EF2=AD·BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com