
分析 利用组合数公式的性质Cn+13-cn3=Cn2,可得 C22+C32+C42+…+C192 =C33 +(C43-C33)+(C53-C43)+…+(C203-C193),化简得到结果.
解答 解:C${\;}_{2}^{0}$+C${\;}_{3}^{1}$+C${\;}_{4}^{2}$+C${\;}_{5}^{3}$+C${\;}_{6}^{4}$+…+C${\;}_{18}^{16}$+C${\;}_{19}^{17}$
=${C}_{2}^{2}$+${C}_{3}^{2}$+${C}_{4}^{2}$+${C}_{5}^{2}$+${C}_{6}^{2}$+…+${C}_{18}^{2}$+${C}_{19}^{2}$,
∵Cn+13-cn3=Cn2,
∴C22+C32+C42+…+C192
=C33 +(C43-C33)+(C53-C43)+…+(C203-C193)
=C203 =$\frac{20×19×18}{3×2}$=1140,
故答案为:1140.
点评 本题主要考查组合数公式的性质应用,利用了组合数公式的性质Cn+13-cn3=Cn2,即Cn2 +cn3 =Cn+13,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 48 | B. | 36 | C. | 30 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-1或1<x<2} | B. | {x|1<x<2} | C. | {x|-1<x<2且x≠1} | D. | {x|x<2且x≠1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
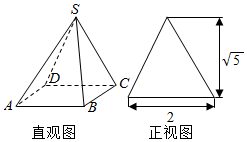
| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,AC交BD于点O,PD=PC=$\sqrt{2}$,PB=2,M为PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,AC交BD于点O,PD=PC=$\sqrt{2}$,PB=2,M为PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 2 | C. | -1或2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -i | B. | i | C. | $\frac{1}{2}$+$\frac{1}{2}$i | D. | $\frac{1}{2}$-$\frac{1}{2}$i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com