
(1)用数学归纳法证明:an>2(n∈N*);
(2)对于n∈N*,证明:
①an+1-2<![]() (an-2);
(an-2);
②a1+a2+a3+…+an<2n+1.
证明:(1)①当n=1时,a1=![]() >2,结论成立.
>2,结论成立.
②假设n=k(k≥1)不等式ak>2成立,
当n=k+1时,ak+1=![]() ,
,
∴ak+1-2=![]() -2=
-2=![]() .
.
由ak>2得ak+1-2>0,即ak+1>2.
说明当n=k+1时,不等式也成立.
根据①和②,可知不等式an>2对于n∈N*都成立.
(2)①由(1)可知an>2(n∈N*),
∴an+1-2>0,an-2>0,
则an+1-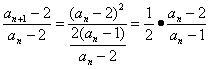 .
.
∵0<an-2<an-1,则0<![]() <1,
<1,
∴![]() <
<![]() ,即an+1-2<
,即an+1-2<![]() (an-2).
(an-2).
②由①可知,当n≥2时,
an-2<![]() (an-1-2)<
(an-1-2)<![]() (an-2-2)<
(an-2-2)<![]() (an-3-2)<…<
(an-3-2)<…<![]() ·(a1-2)=
·(a1-2)=![]() ,
,
则an<2+![]() .
.
∴a1+a2+a3+…+an<(2+![]() )+(2+
)+(2+![]() )+(2+
)+(2+![]() )+…+(2+
)+…+(2+![]() )=2n+(
)=2n+(![]() +
+![]() +
+![]() +…+
+…+![]() )=2n+
)=2n+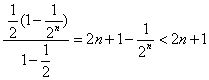 .
.
当n=1时,a1=![]() <2×1+1,不等式也成立,故对于任意n∈N*,都有a1+a2+a3+…+an<2n+1.
<2×1+1,不等式也成立,故对于任意n∈N*,都有a1+a2+a3+…+an<2n+1.


科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| an |
| an |
| n |
| 1 |
| 3 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省汕尾市陆丰市碣石中学高三(上)第四次月考数学试卷(理科)(解析版) 题型:解答题
 ,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn=
,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn= (n∈N*).
(n∈N*). }的前n项和为Tn,证明:
}的前n项和为Tn,证明: .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com