
设集合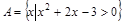 ,集合
,集合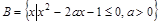 .若
.若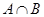 中恰含有一个整数,则实数
中恰含有一个整数,则实数 的取值范围是( )
的取值范围是( )
A.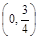 | B.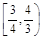 | C.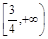 | D.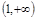 |
B
解析试题分析:先求解一元二次不等式化简集合A,B,然后分析集合B的左端点的大致位置,结合A∩B中恰含有一个整数得集合B的右端点的范围,列出无理不等式组后进行求解解:由x2+2x-3>0,得:x<-3或x>1.由x2-2ax-1≤0,得:a- ≤x≤a+
≤x≤a+ .所以,A={x|x2+2x-3>0}={x|x<-3或x>1},B={x|x2-2ax-1≤0,a>0}={x|a-
.所以,A={x|x2+2x-3>0}={x|x<-3或x>1},B={x|x2-2ax-1≤0,a>0}={x|a- ≤x≤a+
≤x≤a+ }.因为a>0,所以a+1>
}.因为a>0,所以a+1> ,则a-
,则a- >-1且小于0.由A∩B中恰含有一个整数,所以2≤a+
>-1且小于0.由A∩B中恰含有一个整数,所以2≤a+ <3.解得所以,满足A∩B中恰含有一个整数的实数a的取值范围是
<3.解得所以,满足A∩B中恰含有一个整数的实数a的取值范围是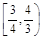 ,选B.
,选B.
考点:交集及其运算
点评:本题考查了交集及其运算,考查了数学转化思想,训练了无理不等式的解法,求解无理不等式是该题的一个难点.此题属中档题.


科目:高中数学 来源: 题型:单选题
已知集合M={ x︱0≤x<2 },N={ x︱ <0 },则集合M∩N=( )
<0 },则集合M∩N=( )
A{x︱0≤x<1} B{x ︱ 0≤x≤1}
C{x︱0≤x<2} D{ x︱ 0≤x≤2 }
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com