
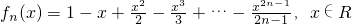 .
.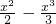 -kx,
-kx, 时,△≤0,y′=-(x2-x+k+1)≤0,
时,△≤0,y′=-(x2-x+k+1)≤0, 时,方程x2-x+k+1=0的两根为
时,方程x2-x+k+1=0的两根为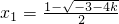 ,
, ,
, -
- +…-
+…-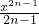 ,
,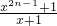 ,
, )+(
)+( )+…+(
)+…+(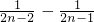 )>0,
)>0,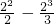 )+(
)+(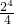 -
-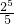 )+…+(
)+…+(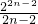 -
-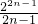 )
) )•22+(
)•22+(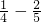 )•24+…+
)•24+…+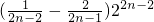
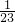 •22-
•22-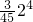 -…-
-…- <0,
<0,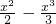 -kx,求导数y′,按△≤0,△>0两种情况讨论,△≤0时y′≤0,可知函数在R上的单调性;当△>0时解不等式y′>0,y′<0即得函数的单调区间;
-kx,求导数y′,按△≤0,△>0两种情况讨论,△≤0时y′≤0,可知函数在R上的单调性;当△>0时解不等式y′>0,y′<0即得函数的单调区间;

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
| x2 |
| 2 |
| x3 |
| 3 |
| x2n-1 |
| 2n-1 |
查看答案和解析>>
科目:高中数学 来源:2006-2007学年广东省阳江市高三(上)期末数学试卷(理科)(解析版) 题型:解答题
 对一切n∈N*均成立的最大实数a;
对一切n∈N*均成立的最大实数a;查看答案和解析>>
科目:高中数学 来源:广州一模 题型:解答题
| x2 |
| 2 |
| x3 |
| 3 |
| x2n-1 |
| 2n-1 |
查看答案和解析>>
科目:高中数学 来源:2013年广东省广州市高考数学一模试卷(文科)(解析版) 题型:解答题
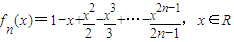 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com