
ЗжЮі ЃЈЂёЃЉЩшГіЖЏЕуNЃЈxЃЌyЃЉЃЌAЃЈx0ЃЌy0ЃЉЃЌMЃЈx0ЃЌ0ЃЉЃЌгЩЬтвтЧѓдВC1ЕФЗНГЬЃЌНсКЯвбжЊ$\overrightarrow{ON}=\frac{2}{3}\overrightarrow{OA}+ЃЈ{\frac{{2\sqrt{2}}}{3}-\frac{2}{3}}ЃЉ\overrightarrow{OM}$ЃЌАбAЕФзјБъгУNЕФзјБъБэЪОЃЌДњШыдВЕФЗНГЬЧѓЕУЭждВCЕФЗНГЬЃЛ
ЃЈЂђЃЉМйЩшжБЯпlЕФаБТЪДцдкЪБЃЌЩшЦфЗНГЬЮЊy=kx+mЃЌСЊСЂжБЯпЗНГЬКЭЭждВЗНГЬЃЌРћгУ$\overrightarrow{OA}•\overrightarrow{OB}=0$ЃЌНсКЯИљдЁЯЕЪ§ЕФЙиЯЕЕУЕН3m2=8k2+8ЃЎдйРћгУЯвГЄЙЋЪНЧѓЕУЯвABЕФГЄЃЌРћгУЛљБОВЛЕШЪНМАКЏЪ§ЕФаджЪЧѓЕУ|AB|ЕФЗЖЮЇЃЛШєжБЯпlЕФаБТЪВЛДцдкЃЌжБНгЧѓГіAЃЌBЕФзјБъЕУЕН|AB|ЕФжЕЃЌдђЯпЖЮABГЄЖШЕФШЁжЕЗЖЮЇПЩЧѓЃЎ
НтД№ НтЃКЃЈЂёЃЉЩшЖЏЕуNЃЈxЃЌyЃЉЃЌAЃЈx0ЃЌy0ЃЉЃЌ
ЁпAMЁЭxжсгкЕуMЃЌЁрMЃЈx0ЃЌ0ЃЉЃЌ
ЩшдВC1 ЕФЗНГЬЮЊx2+y2=r2ЃЌгЩЬтвтЕУ$r=\frac{|3\sqrt{5}|}{\sqrt{1+4}}=3$ЃЌ
ЁрдВC1 ЕФЗНГЬЮЊx2+y2=9ЃЎ
гЩЬтвтЃЌ$\overrightarrow{ON}=\frac{2}{3}\overrightarrow{OA}+ЃЈ{\frac{{2\sqrt{2}}}{3}-\frac{2}{3}}ЃЉ\overrightarrow{OM}$ЃЌЕУ$ЃЈxЃЌyЃЉ=\frac{2}{3}ЃЈ{x}_{0}ЃЌ{y}_{0}ЃЉ+ЃЈ\frac{2\sqrt{2}}{3}-\frac{2}{3}ЃЉЃЈ{x}_{0}ЃЌ0ЃЉ$ЃЌ
Ёр$\left\{\begin{array}{l}{x=\frac{2\sqrt{2}}{3}{x}_{0}}\\{y=\frac{2}{3}{y}_{0}}\end{array}\right.$ЃЌМД$\left\{\begin{array}{l}{{x}_{0}=\frac{3}{2\sqrt{2}}x}\\{{y}_{0}=\frac{3}{2}y}\end{array}\right.$ЃЌ
НЋAЃЈ$\frac{3}{2\sqrt{2}}xЃЌ\frac{3}{2}y$ЃЉДњШыx2+y2=9ЃЌЕУЖЏЕуNЕФЙьМЃЗНГЬЮЊ$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$ЃЛ
ЃЈЂђЃЉЃЈ1ЃЉМйЩшжБЯпlЕФаБТЪДцдкЃЌЩшЦфЗНГЬЮЊy=kx+mЃЌ
СЊСЂ$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+2{y}^{2}=8}\end{array}\right.$ЃЌПЩЕУЃЈ1+2k2ЃЉx2+4kmx+2m2-8=0ЃЎ
ЁрЁї=64k2-8m2+32ЃО0ЃЎ
${x}_{1}+{x}_{2}=-\frac{4km}{1+2{k}^{2}}ЃЌ{x}_{1}{x}_{2}=\frac{2{m}^{2}-8}{1+2{k}^{2}}$ЃЌЃЈ*ЃЉ
Ёп$\overrightarrow{OA}ЁЭ\overrightarrow{OB}$ЃЌЁр$\overrightarrow{OA}•\overrightarrow{OB}=0$ЃЌдђx1x2+ЃЈkx1+mЃЉЃЈkx2+mЃЉ=0ЃЌ
ЛЏМђПЩЕУЃЌ$ЃЈ{k}^{2}+1ЃЉ{x}_{1}{x}_{2}+kmЃЈ{x}_{1}+{x}_{2}ЃЉ+{m}^{2}=0$ЃЎ
НЋЃЈ*ЃЉДњШыПЩЕУ3m2=8k2+8ЃЎ
гжЁп|AB|=$\sqrt{1+{k}^{2}}|{x}_{1}-{x}_{2}|=\sqrt{1+{k}^{2}}\frac{\sqrt{64{k}^{2}-8{m}^{2}32}}{1+2{k}^{2}}$ЃЎ
НЋ${m}^{2}=\frac{8}{3}ЃЈ{k}^{2}+1ЃЉ$ДњШыЃЌПЩЕУ$|AB|=\sqrt{1+{k}^{2}}•\frac{\sqrt{\frac{2ЁС64{k}^{2}}{3}+\frac{32}{3}}}{1+2{k}^{2}}$=$\sqrt{\frac{32}{3}}•\sqrt{1+\frac{{k}^{2}}{1+4{k}^{4}+4{k}^{2}}}$
=$\sqrt{\frac{32}{3}}•\sqrt{1+\frac{1}{\frac{1}{{k}^{2}}+4{k}^{2}+4}}$$Ём2\sqrt{3}$ЃЎ
ЁрЕБЧвНіЕБ${k}^{2}=\frac{1}{2}$ЃЌМД$k=ЁР\frac{\sqrt{2}}{2}$ЪБЕШКХГЩСЂЃЎ
гжгЩ$\frac{{k}^{2}}{1+4{k}^{4}+4{k}^{2}}Ён0$ЃЌЁр|AB|$Ён\sqrt{\frac{32}{3}}=\frac{4\sqrt{6}}{3}$ЃЎ
Ёр$\frac{4\sqrt{6}}{3}Ём|AB|Ём2\sqrt{3}$ЃЎ
ЃЈ2ЃЉШєжБЯпlЕФаБТЪВЛДцдкЃЌдђOAЫљдкжБЯпЗНГЬЮЊy=xЃЌ
СЊСЂ$\left\{\begin{array}{l}{y=x}\\{{x}^{2}+2{y}^{2}=8}\end{array}\right.$ЃЌНтЕУAЃЈ$\frac{2\sqrt{6}}{3}ЃЌ\frac{2\sqrt{6}}{3}$ЃЉЃЌ
ЭЌРэЧѓЕУBЃЈ$\frac{2\sqrt{6}}{3}ЃЌ-\frac{2\sqrt{6}}{3}$ЃЉЃЌ
ЧѓЕУ$|AB|=\frac{4\sqrt{6}}{3}$ЃЎ
злЩЯЃЌЕУ$\frac{4\sqrt{6}}{3}Ём|AB|Ём2\sqrt{3}$ЃЎ
ЕуЦР БОЬтЪЧжБЯпгыдВЃЌжБЯпгыдВзЖЧњЯпЕФзлКЯЬтЃЌПМВщжБЯпКЭдВЕФЮЛжУЙиЯЕЃЌПМВщСЫжБЯпгыЭждВЕФЮЛжУЙиЯЕЃЌбЕСЗСЫЯђСПдкЧѓНтжБЯпгыдВзЖЧњЯпЮЪЬтжаЕФгІгУЃЌПМВщСЫЯвГЄЙЋЪНЕФдЫгУЃЌбЕСЗСЫРћгУВЛЕШЪНЧѓНтзюжЕЮЪЬтЃЌзлКЯадЧПЃЌФбЖШНЯДѓЃЎ


 ШЋгХЕуСЗЕЅдЊМЦЛЎЯЕСаД№АИ
ШЋгХЕуСЗЕЅдЊМЦЛЎЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
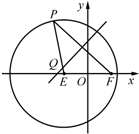 ШчЭМЃЌвбжЊдВEЃК${ЃЈx+\sqrt{3}ЃЉ^2}+{y^2}$=16ЃЌЕу$FЃЈ\sqrt{3}ЃЌ0ЃЉ$ЃЌPЪЧдВEЩЯШЮвтвЛЕуЃЎЯпЖЮPFЕФДЙжБЦНЗжЯпКЭАыОЖPEЯрНЛгкQЃЎ
ШчЭМЃЌвбжЊдВEЃК${ЃЈx+\sqrt{3}ЃЉ^2}+{y^2}$=16ЃЌЕу$FЃЈ\sqrt{3}ЃЌ0ЃЉ$ЃЌPЪЧдВEЩЯШЮвтвЛЕуЃЎЯпЖЮPFЕФДЙжБЦНЗжЯпКЭАыОЖPEЯрНЛгкQЃЎВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com