
【题目】如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点.
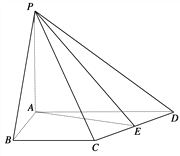
(1)证明:CD⊥平面PAE;
(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(Ⅰ)要证![]() 平面
平面![]() ,由已知
,由已知![]() 平面
平面![]() ,已经有
,已经有![]() ,因此在直角梯形
,因此在直角梯形![]() 中证明
中证明![]() 即可,通过计算得
即可,通过计算得![]() ,而
,而![]() 是
是![]() 中点,则有
中点,则有![]() ;(Ⅱ)PB与平面ABCD所成的角是
;(Ⅱ)PB与平面ABCD所成的角是![]() ,下面关键是作出PB与平面PAE所成的角,由(Ⅰ)作
,下面关键是作出PB与平面PAE所成的角,由(Ⅰ)作![]() ,分别与
,分别与![]() 相交于
相交于![]() ,连接
,连接![]() ,则
,则![]() 是PB与平面PAE所成的角,由这两个角相等,可得
是PB与平面PAE所成的角,由这两个角相等,可得![]() ,同样在直角梯形
,同样在直角梯形![]() 中可计算出
中可计算出![]() ,也即四棱锥P-ABCD的高,体积可得.另外也可建立空间直角坐标系,通过空间向量法求得结论,第(Ⅱ)小题中关键是求点
,也即四棱锥P-ABCD的高,体积可得.另外也可建立空间直角坐标系,通过空间向量法求得结论,第(Ⅱ)小题中关键是求点![]() 的坐标,注意这里直线与平面所成的角相等转化为直线与平面的法向量的夹角相等.
的坐标,注意这里直线与平面所成的角相等转化为直线与平面的法向量的夹角相等.
试题解析:解法1(Ⅰ如图(1)),连接AC,由AB=4,![]() ,
,![]()
![]()
![]() 是
是![]() 的中点,所以
的中点,所以![]()
![]() 所以
所以![]()
而![]() 内的两条相交直线,所以CD⊥平面PAE.
内的两条相交直线,所以CD⊥平面PAE.
(Ⅱ)过点B作![]()
由(Ⅰ)CD⊥平面PAE知,BG⊥平面PAE.于是![]() 为直线PB与平面PAE
为直线PB与平面PAE
所成的角,且![]() .
.
由![]() 知,
知,![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角.
所成的角.
![]() 由题意,知
由题意,知![]()
因为![]() 所以
所以![]()
由![]() 所以四边形
所以四边形![]() 是平行四边形,故
是平行四边形,故![]() 于是
于是![]()
在![]() 中,
中,![]() 所以
所以
![]()
于是![]()
又梯形![]() 的面积为
的面积为![]() 所以四棱锥
所以四棱锥![]() 的体积为
的体积为
![]()
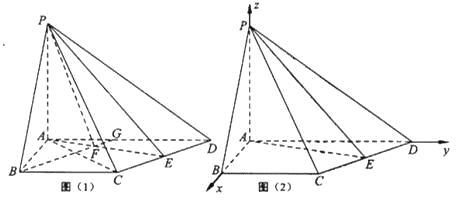
解法2:如图(2),以A为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 建立空间直角坐标系.设
建立空间直角坐标系.设![]() 则相关的各点坐标为:
则相关的各点坐标为:
![]()
(Ⅰ)易知![]() 因为
因为
![]() 所以
所以![]() 而
而![]() 是平面
是平面![]() 内的两条相交直线,所以
内的两条相交直线,所以![]()
(Ⅱ)由题设和(Ⅰ)知,![]() 分别是
分别是![]() ,
,![]() 的法向量,而PB与
的法向量,而PB与
![]() 所成的角和PB与
所成的角和PB与![]() 所成的角相等,所以
所成的角相等,所以
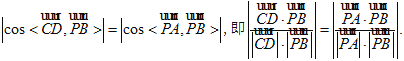
由(Ⅰ)知,![]() 由
由![]() 故
故
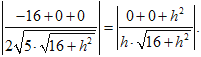
解得![]() .
.
又梯形ABCD的面积为![]() ,所以四棱锥
,所以四棱锥![]() 的体积为
的体积为
![]() .
.


科目:高中数学 来源: 题型:
【题目】已知点A、B、C的坐标分别为A(3,0)、B(0,3)、C(cosα,sinα),α∈(![]() ,
,![]() ).
).
(1)若|![]() |=|
|=|![]() |,求角α的值;
|,求角α的值;
(2)若![]() ·
·![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了保护环境,发展低碳经济,在国家科研部门的支持下,进行技术攻关,新上了一个把二氧化碳处理转化为一种化工产品的项目,经测算,该项目月处理成本![]() (单位:元)与月处理量
(单位:元)与月处理量![]() (单位:吨)之间的函数关系可近似地表示为
(单位:吨)之间的函数关系可近似地表示为![]() ,且每处理一吨二氧化碳所得的这种化工产品可获利
,且每处理一吨二氧化碳所得的这种化工产品可获利![]() 元,如果该项目不获利,那么亏损数额将由国家给予补偿.
元,如果该项目不获利,那么亏损数额将由国家给予补偿.
(![]() )求
)求![]() 时,该项目的月处理成本.
时,该项目的月处理成本.
(![]() )当
)当![]() 时,判断该项目能否获利?如果亏损,那么国家每月补偿数额(单位:元)的范围是多少?
时,判断该项目能否获利?如果亏损,那么国家每月补偿数额(单位:元)的范围是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论
①AC⊥BD;
②△ACD是等边三角形;
③AB与平面BCD成60°的角;
④AB与CD所成的角是60°.
其中正确结论的序号是________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1,2,3,4,…,30这30个自然数中任选1个数,求下列事件的概率:
(1)取出的数为偶数;
(2)取出的数能被3整除;
(3)取出的数能被5整除;
(4)取出的数大于8;
(5)取出的数大于8或是偶数;
(6)取出的数能被3或5整除;
(7)取出的数是能被3整除的偶数;
(8)取出的数是偶数或能被5整除.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,周期是
,周期是![]() .
.
(1)求函数解析式,并写出函数图象的对称轴方程和对称中心;
(2)已知点![]() ,点
,点![]() 是该函数图象上一点,点
是该函数图象上一点,点![]() 是
是![]() 的中点,当
的中点,当![]() ,
, ![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com