
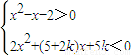 的解集中所含整数解只有-2,求k的取值范围 .
的解集中所含整数解只有-2,求k的取值范围 .  的大小关系,综合讨论结果,可得答案.
的大小关系,综合讨论结果,可得答案. 时,2x2+(5+2k)x+5k<0的解集为(-
时,2x2+(5+2k)x+5k<0的解集为(- ,-k),
,-k), 的解集中所含整数解只有-2
的解集中所含整数解只有-2 时,2x2+(5+2k)x+5k<0的解集为∅,不满足要求
时,2x2+(5+2k)x+5k<0的解集为∅,不满足要求 时,2x2+(5+2k)x+5k<0的解集为(-k,-
时,2x2+(5+2k)x+5k<0的解集为(-k,- ),不满足要求
),不满足要求

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com