
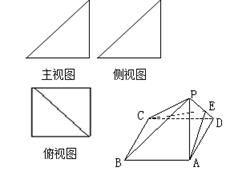
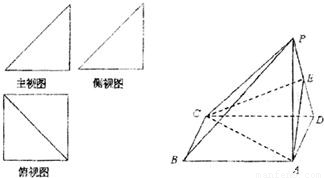
一个简单多面体的直观图和三视图如图所示,它的主视图和侧视图都是腰长为1的等腰直角三角形,俯视图为正方形,E是PD的中点.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
(1)见解析(2)见解析(3)![]()
(1)证明:依题意,该三视图所对应的直观图为一侧棱PA垂直于底面ABCD的四棱锥,且PA=AB=AD=1,四边形ABCD为正方形;
分别连结AC、BD交于O,连结EO,∵E是PD的中点,∴PB∥EO,
又PB![]() 平面ACE,EO
平面ACE,EO![]() 平面ACE,∴PB∥平面ACE。…………4分
平面ACE,∴PB∥平面ACE。…………4分
(2)证明:∵四边形ABCD是正方形,∴BD⊥AC,又PA⊥平面ABCD,
∴BD⊥PA,又∵PA∩AC=A,∴BD⊥平面PAC,
又PC![]() 平面PAC,PC⊥BD。…………9分
平面PAC,PC⊥BD。…………9分  w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m
(3)∵PA⊥平面ABCD,PA=AB=BC=1,∴VC—PAB=VP—ACD=![]() ×SΔABC×PA=
×SΔABC×PA=![]() ×
×![]() ×1×1×1=
×1×1×1=![]() 。∴三棱锥C—PAB的体积为
。∴三棱锥C—PAB的体积为![]() 。…………14分
。…………14分


科目:高中数学 来源: 题型:
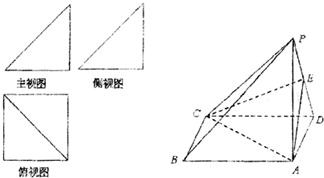 一个简单多面体的直观图和三视图如图所示,它的主视图和侧视图都是腰长为1的等腰直角三角形,俯视图为正方形,E是PD的中点.
一个简单多面体的直观图和三视图如图所示,它的主视图和侧视图都是腰长为1的等腰直角三角形,俯视图为正方形,E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
一个简单多面体的直观图和三视图如图所示,它的主视图和侧视图都是腰长为1的等腰直角三角形,俯视图为正方形,E是PD的中点.
(Ⅰ)求证:PB∥平面ACE;
(Ⅱ)求证:PC⊥BD;
(Ⅲ)求三棱![]() 锥C-PAB的体积.
锥C-PAB的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
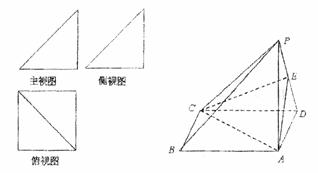
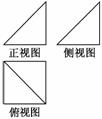
一个简单多面体的直观图和三视图如图所示,它的正视图和侧视图都是腰长为1的等腰直角三角形,俯视图为正方形,E是PD的中点.
(1)求证:PB∥平面ACE;
(2)求证:PC⊥BD;
(3)求三棱锥C-PAB的体积.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省金华市兰溪三中高二(上)期中数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com