
 ]∪[-1,+∞)
]∪[-1,+∞)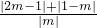 恒成立,又因为根据绝对值不等式可得到右边大于等于1.即可得到|x-1|-|2x+3|≤1,分类讨论去绝对值号即可求得x的取值范围.
恒成立,又因为根据绝对值不等式可得到右边大于等于1.即可得到|x-1|-|2x+3|≤1,分类讨论去绝对值号即可求得x的取值范围.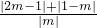 恒成立,∵
恒成立,∵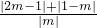 ≥
≥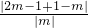 =1,
=1, 时,原式1-x+2x+3≤1,即x≤-3,所以x≤-3
时,原式1-x+2x+3≤1,即x≤-3,所以x≤-3 <x<1时,原式1-x-2x-3≤1,即x≥-1,所以-1≤x<1
<x<1时,原式1-x-2x-3≤1,即x≥-1,所以-1≤x<1 ]∪[-1,+∞).
]∪[-1,+∞).

科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 4 |
| ||
| 2 |
| 2 |
| x |
查看答案和解析>>
科目:高中数学 来源:河南省焦作市2012届高三第一次质量检测数学理科试题 题型:022
若对于任意非零实数m,不等式|2m-1|+|1-m|>|m|(|x|-|x|)恒成立,则实数x的取值范围________.
查看答案和解析>>
科目:高中数学 来源:2012年河南省焦作市高三第一次质量检测数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com