已知等差数列an的前n项和为Sn,若(a2-1)3+5(a2-1)=1,(a2010-1)3+5(a2010-1)=-1,则a2+a2010=________S2011=________.
2 2011
分析:由(a
2-1)
3+5(a
2-1)=1,(a
2010-1)
3+5(a
2010-1)=-1,可得0<a
2-1<1,-1<a
2010-1<0
由0<a
2-1<1,-1<a
2010-1<0 可得(a
2-1)
2+(a
2010-1)
2-(a
2-1)(a
2010-1)+5>0
从而可求,a
2+a
2010=2
由等差数列的前n项和及等差数列的性质可得,
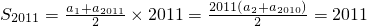
解答:由(a
2-1)
3+5(a
2-1)=1,(a
2010-1)
3+5(a
2010-1)=-1,可得
0<a
2-1<1,-1<a
2010-1<0
两式相加可得并整理可得,(a
2+a
2010-2)[(a
2-1)
2+(a
2010-1)
2-(a
2-1)(a
2010-1)+5]=0
由0<a
2-1<1,-1<a
2010-1<0
可得(a
2-1)
2+(a
2010-1)
2-(a
2-1)(a
2010-1)+5>0
∴a
2+a
2010=2
由等差数列的前n项和及等差数列的性质可得,
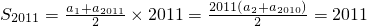
故答案为:2;2011
点评:本题主要考查了等差数列的性质:若m+n=p+q 则a
p+a
q=a
n+a
m;等差数列的前n项和公式
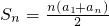
,考查了推理运算的能力.

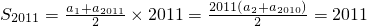
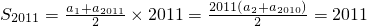
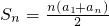 ,考查了推理运算的能力.
,考查了推理运算的能力. 

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案