
【题目】如图,四边形ABCD与BDEF均为菱形,设AC与BD相交于点O,若∠DAB=∠DBF=60°,且FA=FC.
(1)求证:FC∥平面EAD;
(2)求二面角A-FC-B的余弦值.

【答案】(1)见解析(2)![]()
【解析】
(1)先证明平面FBC∥平面EAD,即证明FC∥平面EAD.(2)利用向量法求二面角A-FC-B的余弦值.
(1)证明:∵四边形ABCD与BDEF均为菱形,
∴AD∥BC,DE∥BF.
∵AD平面FBC,DE平面FBC,
∴AD∥平面FBC,DE∥平面FBC,
又AD∩DE=D,AD平面EAD,DE平面EAD,
∴平面FBC∥平面EAD,
又FC平面FBC,∴FC∥平面EAD.
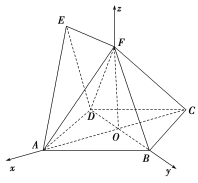
(2)连接FO、FD,∵四边形BDEF为菱形,且∠DBF=60°,∴△DBF为等边三角形,
∵O为BD中点.所以FO⊥BD,O为AC中点,且FA=FC,
∴AC⊥FO,
又AC∩BD=O,∴FO⊥平面ABCD,
∴OA、OB、OF两两垂直,建立如图所示的空间直角坐标系O-xyz,
设AB=2,因为四边形ABCD为菱形,∠DAB=60°,
则BD=2,OB=1,OA=OF=![]() ,
,
∴O(0,0,0),A(![]() ,0,0),B(0,1,0),C(-
,0,0),B(0,1,0),C(-![]() ,0,0),F(0,0,
,0,0),F(0,0,![]() ),
),
∴![]() =(
=(![]() ,0,
,0,![]() ),
),![]() =(
=(![]() ,1,0),
,1,0),
设平面BFC的一个法向量为n=(x,y,z),
则有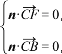 ∴
∴![]()
令x=1,则n=(1,-![]() ,-1),
,-1),
∵BD⊥平面AFC,∴平面AFC的一个法向量为![]() =(0,1,0).
=(0,1,0).
∵二面角A-FC-B为锐二面角,设二面角的平面角为θ,
∴cosθ=|cos〈n,![]() 〉|=
〉|=![]() =
=![]() =
=![]() ,
,
∴二面角A-FC-B的余弦值为![]() .
.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】某大学志愿者协会有6名男同学,4名女同学.在这10名同学中,3名同学来自数学学院,其余7名同学来自物理、化学等其他互不相同的七个学院.现从这10名同学中随机选取3名同学,到希望小学进行支教活动(每位同学被选到的可能性相同).
(1)求选出的3名同学是来自互不相同学院的概率;
(2)设![]() 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的表格中,每格填上一个数字后,使每一横行成等差数列,每一纵列成等比数列,则a+b+c的值为( )
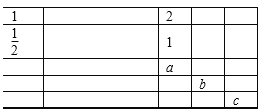
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A=a1 , a2 , a3 , …,an , 其中ai∈R(1≤i≤n,n>2),l(A)表示和ai+aj(1≤i<j≤n)中所有不同值的个数.
(Ⅰ)设集合P=2,4,6,8,Q=2,4,8,16,分别求l(P)和l(Q);
(Ⅱ)若集合A=2,4,8,…,2n , 求证: ![]() ;
;
(Ⅲ)l(A)是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中错误的个数为:( )
①![]() 的图像关于点
的图像关于点![]() 对称;②
对称;②![]() 的图像关于点
的图像关于点![]() 对称;
对称;
③![]() 的图像关于直线
的图像关于直线![]() 对称;④
对称;④![]() 的图像关于直线
的图像关于直线![]() 对称。
对称。
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,直线
,直线![]() .
.
(1)若直线![]() 与圆
与圆![]() 相切,求
相切,求![]() 的值;
的值;
(2)若直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,当∠AOB为锐角时,求k的取值范围;
,当∠AOB为锐角时,求k的取值范围;
(3)若![]() ,
,![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作圆
作圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,探究:直线
,探究:直线![]() 是否过定点。
是否过定点。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲厂以x千克/小时的速度匀速生产某种产品(生产条件要求1≤x≤10),每小时可获得的利润是100(5x+1﹣ ![]() )元.
)元.
(1)要使生产该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求此最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com