
 如图,已知一个圆锥的底面半径为R,高为h,在其中有一个高为x的内接圆柱(其中R,h均为常数).
如图,已知一个圆锥的底面半径为R,高为h,在其中有一个高为x的内接圆柱(其中R,h均为常数).| 2 | 3 |
| h |
| R |
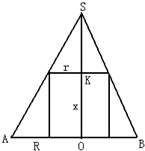 解:圆锥、圆柱的轴截面如图所示,其中SO=h,OA=OB=R,OK=x.
解:圆锥、圆柱的轴截面如图所示,其中SO=h,OA=OB=R,OK=x.| r |
| R |
| h-x |
| h |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 3 |
| 1 |
| 81 |
| h |
| R |
| h |
| R |
| 2πR |
| h |
| h |
| 2 |
| πRh |
| 2 |
| h |
| 2 |
| πRh |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 如图,已知一个圆锥的底面半径为R=1,高为h=2.,一个圆柱的下底面在圆锥的底面上,且圆柱的上底面为圆锥的截面,设圆柱的高为x.
如图,已知一个圆锥的底面半径为R=1,高为h=2.,一个圆柱的下底面在圆锥的底面上,且圆柱的上底面为圆锥的截面,设圆柱的高为x.查看答案和解析>>
科目:高中数学 来源: 题型:
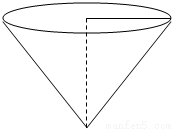
 用铁皮制作一个无盖的圆锥形容器,如图,已知该圆锥的母线与底面所在平面的夹角为45°,容器的高为10cm.制作该容器需要多少面积的铁皮?该容器的容积又是多少?(衔接部分忽略不计,结果精确到0.1cm2)
用铁皮制作一个无盖的圆锥形容器,如图,已知该圆锥的母线与底面所在平面的夹角为45°,容器的高为10cm.制作该容器需要多少面积的铁皮?该容器的容积又是多少?(衔接部分忽略不计,结果精确到0.1cm2)查看答案和解析>>
科目:高中数学 来源:2013届上海市高二年级期终考试数学 题型:解答题
(本题满分12分)
用铁皮制作一个无盖的圆锥形容器,如图,已知该圆锥的母线与底面所在平面的夹角为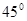 ,容器的高为
,容器的高为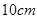 .制作该容器需要多少面积的铁皮?该容器的容积又是多少?(衔接部分忽略不计,结果精确到
.制作该容器需要多少面积的铁皮?该容器的容积又是多少?(衔接部分忽略不计,结果精确到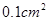 )
)
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省徐州市高二(上)期中数学试卷(文科)(解析版) 题型:解答题
 h时,求内接圆柱上方的圆锥的体积V;
h时,求内接圆柱上方的圆锥的体积V;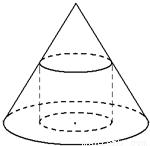
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com