
分析 把球的球心连接,则又可得到一个棱长为2的小正四面体,正四面体的中心到底面的距离是高的,且小正四面体的中心和正四面体容器的中心应该是重合的,先求出小正四面体的中心到底面的距离,再求出正四面体的中心到底面的距离,把此距离乘以4可得正四棱锥的高,再根据正四面体的棱长与高的关系求得棱长..
解答 解:由题意知,底面放三个球,上再落一个球.于是把球的球心连接,则又可得到一个棱长为2的小正四面体,则不难求出这个小正四面体的高为$\frac{\sqrt{6}}{3}a=\frac{2\sqrt{6}}{3}$,
且由正四面体的性质可知:正四面体的中心到底面的距离是高的$\frac{1}{4}$,且小正四面体的中心和正四面体容器的中心应该是重合的,
∴小正四面体的中心到底面的距离$\frac{2\sqrt{6}}{3}×\frac{1}{4}=\frac{\sqrt{6}}{6}$=,正四面体的中心到底面的距离是$\frac{\sqrt{6}}{6}+1$,所以可知正四面体的高的最小值为($\frac{\sqrt{6}}{6}$+1)×4=4+$\frac{2\sqrt{6}}{3}$,
设正四面体的棱长为m,$\frac{\sqrt{6}}{3}m=4+\frac{2\sqrt{6}}{3}$,解得m=$2+2\sqrt{6}$,
故答案为:2+2$\sqrt{6}$.
点评 本题考查了正四面体与球心的相切问题,小球的半径与两个四面体棱长的关系,是解题的关键,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 若m∥n,n?α,则 m∥α | B. | 若α⊥β,α∩β=m,m⊥n,则 n⊥α | ||
| C. | 若l⊥n,m⊥n,则 l∥m | D. | 若l⊥α,m⊥β,且 l⊥m,则 α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“如果p2+q2=2,则p+q≤2”的否命题是“如果p+q>2,则p2+q2≠2” | |
| B. | 命题p:?x∈[0,1],ex≥1,命题q:?x∈R,x2+x+1<0,则p∨q为假 | |
| C. | “若am2<bm2,则a<b”的逆命题为真命题 | |
| D. | 若${(\sqrt{x}-\frac{1}{{2\root{3}{x}}})^n}$的展开式中第四项为常数项,则n=5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
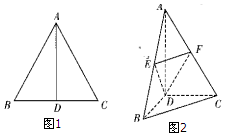 如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.
如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢户外活动 | 不喜欢户外活动 | 合计 | |
| 男性 | 20 | 5 | 25 |
| 女性 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①简单随机抽样,②系统抽样,③分层抽样 | |
| B. | ①分层抽样,②系统抽样,③简单随机抽样 | |
| C. | ①系统抽样,②简单随机抽样,③分层抽样 | |
| D. | ①简单随机抽样,②分层抽样,③系统抽样 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com