
对于定义域为A的函数f(x),如果任意的x1,x2∈A,当x1<x2时,都有f(x1)<f(x2),则称函数f(x)是A上的严格增函数;函数f(k)是定义在N*上,函数值也在N*中的严格增函数,并且满足条件f(f(k))=3k.
(1)证明:f(3k)=3f(k);
(2)求f(3k-1)(k∈N*)的值;
(3)是否存在p个连续的自然数,使得它们的函数值依次也是连续的自然数;若存在,找出所有的p值,若不存在,请说明理由.
(1)见解析(2)2×3k-1(k∈N*)(3)存在p=3k-1+1
【解析】(1)证明:对k∈N*,f(f(k))=3k,∴f[f(f(k))]=f(3k)①
由已知f(f(k))=3k,∴f[f(f(k))]=3f(k),②
由①、②∴f(3k)=3f(k)
(2)若f(1)=1,由已知f(f(k))=3k得f(1)=3,矛盾;
设f(1)=a>1,∴f(f(1))=f(a)=3,③
由f(k)严格递增,即1<a⇒f(1)<f(a)=3,
∴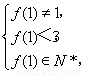 ∴f(1)=2,
∴f(1)=2,
由③f(f(1))=f(a)=3,故f(f(1))=f(2)=3.
∴f(1)=2,f(2)=3.
f(3)=3f(1)=6,f(6)=f(3·2)=3f(2)=9,
f(9)=3f(3)=18,f(18)=3f(6)=27,
f(27)=3f(9)=54,f(54)=3f(18)=81.
依此类推归纳猜出:f(3k-1)=2×3k-1(k∈N*).
下面用数学归纳法证明:
(1)当k=1时,显然成立;
(2)假设当k=l(l≥1)时成立,即f(3l-1)=2×3l-1,
那么当k=l+1时,f(3l)=f(3×3l-1)=3f(3l-1)=3×2×3l-1=2·3l.猜想成立,由(1)、(2)所证可知,对k∈N*f(3k-1)=2×3k-1成立.
(3)存在p=3k-1+1,当p个连续自然数从3k-1→2×3k-1时,函数值正好也是p个连续自然数从f(3k-1)=2×3k-1→f(2×3k-1)=3k.


科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用3练习卷(解析版) 题型:解答题
已知函数f(x)=x2+bx+c(b,c∈R),对任意的x∈R,恒有f′(x)≤f(x).
(1)证明:当x≥0时,f(x)≤(x+c)2;
(2)若对满足题设条件的任意b,c,不等式f(c)-f(b)≤M(c2-b2)恒成立,求M的最小值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用21练习卷(解析版) 题型:填空题
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用1练习卷(解析版) 题型:填空题
已知a=20.5,b=2.10.5,c=log21.5,则a,b,c的大小关系是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用19练习卷(解析版) 题型:解答题
在平面直角坐标系xOy中,已知点A(0,0),B(-2,0),C(-2,1).设k为非零实数,矩阵M=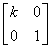 ,N=
,N=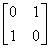 ,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值.
,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用16练习卷(解析版) 题型:解答题
如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.

(1)证明B1C1⊥CE;
(2)求二面角B1-CE-C1的正弦值;
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为 ,求线段AM的长.
,求线段AM的长.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用10练习卷(解析版) 题型:填空题
在正项数列{an}中,a1=2,an+1=2an+3×5n,则数列{an}的通项公式为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com