
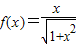 ,数列{an}满足:a1=f(1),an+1=f(an)(n∈N*),则a2010=( )
,数列{an}满足:a1=f(1),an+1=f(an)(n∈N*),则a2010=( )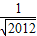
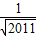
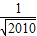
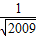
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
| 1 |
| m |
| m |
| m-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)已知函数f(x)满足2ax·f(x)=2f(x)-1,f(1)=1,设无穷数列{an}满足an+1=f(an).(1)求函数f(x)的表达式;(2)若a1=3,从第几项起,数列{an}中的项满足an<an+1;(3)若![]() <a1<
<a1<![]() (m为常数且m∈N+,m≠1),求最小自然数N,使得当n≥N时,总有0<an<1成立。
(m为常数且m∈N+,m≠1),求最小自然数N,使得当n≥N时,总有0<an<1成立。
查看答案和解析>>
科目:高中数学 来源:2011年湖南省益阳市沅江市高三质量检测数学试卷1(理科)(解析版) 题型:解答题
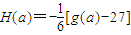 ,数列{an}满足an+1=H(an)(n∈N*),且a1∈(0,1),试判断an+1与an的大小,并证明之.
,数列{an}满足an+1=H(an)(n∈N*),且a1∈(0,1),试判断an+1与an的大小,并证明之.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com