练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

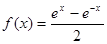    已知函数，函数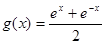，下列关于这两个函数的叙述正确的是（  ）                                               

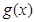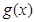    A．是奇函数，是奇函数　　　　B．是奇函数，是偶函数

    C．是偶函数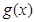，是奇函数        D．是偶函数，是偶函数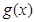

     

    【答案】

    B

    【解析】

    试题分析：易知、的定义域都为R，又，，所以是奇函数，是偶函数，因此选B。

    考点：函数的性质：奇偶性。

    点评：判断一个函数的奇偶性有两步：①求函数的定义域，判断函数的定义域关于原点对称；②判断与的关系。尤其是做大题时不要忘记求函数的定义域。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图所示，给出关于f（x）的下列命题：
    x -1 0 2 4 5
    f（x） 1 2 0 2 1
    ①函数y=f（x）在x=2取到极小值；
    ②函数f（x）在[0，1]是减函数，在[1，2]是增函数；
    ③当1＜a＜2时，函数y=f（x）-a有4个零点；
    ④如果当x∈[-1，t]时，f（x）的最大值是2，那么t的最小值为0．
    其中所有正确命题是
    ①③④
    ①③④
    （写出正确命题的序号）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）的定义域为R，则下列命题中：?
    ①若f（x-2）是偶函数，则函数f（x）的图象关于直线x=2对称；?②若f（x+2）=-f（x-2），则函数f（x）的图象关于原点对称；?③函数y=f（2+x）与函数y=f（2-x）的图象关于直线x=2对称；?④函数y=f（x-2）与函数y=f（2-x）的图象关于直线x=2对称．?
    其中正确的命题序号是
    ④
    ④
    ．?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=sin
    x
    2
     ，  x∈R    ，将函数y=f（x）图象上所有点的横坐标缩短为原来的
    1
    2
    倍（纵坐不变），得到函数g（x）的图象，则关于f（x）•g（x）有下列命题，其中真命题的个数是（　　）
    ①函数y=f（x）•g（x）是奇函数；
    ②函数y=f（x）•g（x）不是周期函数；
    ③函数y=f（x）•g（x）的图象关于点（π，0）中心对称；
    ④函数y=f（x）•g（x）的最大值为
    		3
    3
    ．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年浙江省宁波市八校联考高一（上）数学试卷（解析版） 题型：填空题

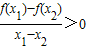    已知函数y=f（x）是R上的偶函数，对于x∈R都有f（x+6）=f（x）+f（3）成立，且f（-6）=-2，当x1，x2∈[0，3]且x1≠x2时，都有，则给出下列命题：
    ①f（2010）=-2；
    ②函数y=f（x）图象的一条对称轴为直线x=-6；
    ③函数y=f（x）在[-9，-6]上为减函数；
    ④函数f（x）在[-9，9]上有4个零点，上述命题中的所有正确命题的序号是    ．（把你认为正确命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源：2014届山东省淄博市高二下学期期中模块检测文科数学试卷（解析版） 题型：选择题

    已知函数的定义域为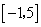，部分对应值如下表：

    的导函数的图象如图所示，

    则下列关于函数的命题：

    ① 函数是周期函数；

    ② 函数在是减函数；

    ③ 如果当时，的最大值是2，那么的最大值为4；

    ④ 当时，函数有4个零点。

    其中真命题的个数是 (    )

    A．4个             B．3个              C．2个              D．1个

     

    查看答案和解析>>

    同步练习册答案