Question

设数列{2^n－1}按第n组有n个数(n是正整数)的规则分组如下：(1)，(2,4)，(8,16,32)，…，则第101组中的第一个数为(　　)

A．2^{4 951}         B．2^{4 950         C}．2^{5 051}      D．2^{5 050}

 

Answer 1

【答案】

D

【解析】本试题主要是考学生灵活运用等比、等差数列的前n项和的公式及等比数列的通项公式化简求值，是一道中档题。

因为第一组数一个数，第二组数有2个，依次可知，第100组有100个数，则可知100组的最后一个数即为以1为首项，公比为2的等比数列的前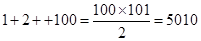，则第101组中的第一个数为2^{5 050}，选D.

解决该试题的关键是根据数列{2^n-1}按“第n组有n个数（n∈N₊）”的规则分组，可知第101组中的第一个数前面有1+2+..+100个数，利用等差数列的前n项和的公式求出数的个数，又因为数列{2^n-1}以1为首项，2为公比的等比数列，写出此等比数列的通项公式，把求出的个数加1代入通项公式中即可得到第101组中的第一个数。