
定义在 上的函数
上的函数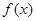 满足以下条件:
满足以下条件:
(1)对任意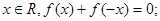 (2)对任意
(2)对任意 .
.
以下不等式:①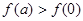 ;②
;②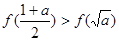 ;③
;③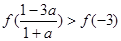 ;④
;④ .其中一定成立的是 (请写出所有正确的序号)
.其中一定成立的是 (请写出所有正确的序号)
①②③
【解析】
试题分析:条件(1)说明是奇函数;条件(2)说明函数在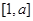 是增函数且函数值为正数。由(1)可知在[-a,-1]函数也为增函数,函数值为负,且有a>1>0.
是增函数且函数值为正数。由(1)可知在[-a,-1]函数也为增函数,函数值为负,且有a>1>0.
因为奇函数在x=0有意义,则f(0)=0,所以结合(2)知①对;
因为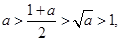 所以
所以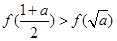 ,②对;
,②对;
因为a>1>0,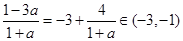 ,且a越大,
,且a越大,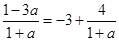 越接近-3,能保证自变量的值在函数的增区间内,所以
越接近-3,能保证自变量的值在函数的增区间内,所以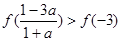 正确,③对;
正确,③对;
对于④,特取a=2时。 , f(-a)=f(2)>0,所以
, f(-a)=f(2)>0,所以 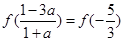 <f(2)矛盾,④不成立。
<f(2)矛盾,④不成立。
综上所述①②③一定成立。
考点:本题主要考查函数的奇偶性、单调性,均值定理的应用。
点评:中档题,对于奇函数,其图象关于原点成中心对称。在关于原点对称的区间,奇函数单调性相同,偶函数单调性相反。


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2009-2010学年湖南省长沙市同升湖实验学校高三(上)第一次月考数学试卷(理科)(解析版) 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京五中高三(上)第二次月考数学试卷(文科)(解析版) 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2011年高三数学(理科)一轮复习讲义:2.3 函数的奇偶性(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2010年高考数学猜题精粹(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com