
【题目】已知圆心(a,b)(a<0,b<0)在直线y=2x+1上的圆,若其圆心到x轴的距离恰好等于圆的半径,在y轴上截得的弦长为 ![]() ,则圆的方程为( )
,则圆的方程为( )
A.(x+2)2+(y+3)2=9
B.(x+3)2+(y+5)2=25
C.![]()
D.![]()
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=k﹣ ![]() (其中k为常数);
(其中k为常数);
(1)求:函数的定义域;
(2)证明:函数在区间(0,+∞)上为增函数;
(3)若函数为奇函数,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=( )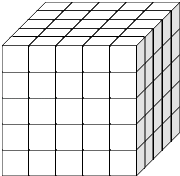
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知 ![]() =(2,1),
=(2,1), ![]() =(1,7),
=(1,7), ![]() =(5,1),设Z是直线OP上的一动点.
=(5,1),设Z是直线OP上的一动点. 
(1)求使 ![]()
![]() 取最小值时的
取最小值时的 ![]() ;
;
(2)对(1)中求出的点Z,求cos∠AZB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x+1)ln x-a(x-1).
(1)当a=4时,求曲线y=f(x)在(1,f(1))处的切线方程;
(2)若当x∈(1,+∞)时,f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述正确的个数是( )
①若a>b,则ac2>bc2;
②若命题p为真命题题,命题q为假命题,则p∨q为假命题;
③若命题p:x0∈R,x ![]() ﹣x0+1≤0,则¬p:x∈R,x2﹣x+1>0.
﹣x0+1≤0,则¬p:x∈R,x2﹣x+1>0.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:x2=2py(p>0),直线y=kx+2与E交于A、B两点,且 ![]()
![]() =2,其中O为原点.
=2,其中O为原点.
(1)求抛物线E的方程;
(2)点C坐标为(0,﹣2),记直线CA、CB的斜率分别为k1 , k2 , 证明:k12+k22﹣2k2为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C所对的边分别是a,b,c,B是钝角,且 ![]() a=2bsinA.
a=2bsinA.
(1)求B的大小;
(2)若△ABC的面积为 ![]() ,且b=7,求a+c的值;
,且b=7,求a+c的值;
(3)若b=6,求△ABC面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com