
 方向行走一段时间后,再向正北方向行走一段时间,但何时改变方向不定.假定机器人行走速度为10米/分钟,则机器人行走2分钟时的可能落点区域面积为________.
方向行走一段时间后,再向正北方向行走一段时间,但何时改变方向不定.假定机器人行走速度为10米/分钟,则机器人行走2分钟时的可能落点区域面积为________.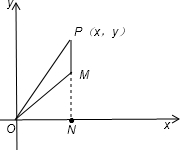 解:设改变方向的点为M,
解:设改变方向的点为M,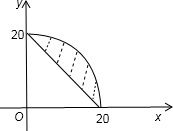 ∴区域S:
∴区域S: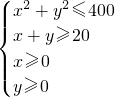 为弓形,
为弓形, π×202-
π×202- ×20×20=100π-200.
×20×20=100π-200.

科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com