
分析 (1)由题意可得1-an+1=1-sin($\frac{π}{2}$an),令bn=1-an,Tn为数列{bn}的前n项和,运用分析法证明,结合x>0时,sinx<x,运用等比数列的求和公式,即可得证;
(2)(Ⅰ)在数列{an}中,a1=1,${a}_{n+1}=c{a}_{n}{+c}^{n+1}(2n+1)$,n∈N*,可得$\frac{{a}_{n+1}}{{c}^{n+1}}$=$\frac{{a}_{n}}{{c}^{n}}$+2n+1,运用数列恒等式,结合等差数列的求和公式,化简即可得到所求;
(Ⅱ)由对一切k∈N*有a2k>a2k-1,可得一切k∈N*有4(c2-c)k2+4ck-c2+c-1>0.设f(x)=4(c2-c)x2+4cx-c2+c-1,求出对称轴和f(1)>0,及c2-c≥0,可得c的范围,证c在这个范围内不等式恒成立.即可得到所求范围.
解答 解:(1)证明:数列{an}中,${a_1}=\frac{1}{2}$,${a_{n+1}}=sin({\frac{π}{2}{a_n}})({n∈{{N}^*}})$,
可得1-an+1=1-sin($\frac{π}{2}$an),
令bn=1-an,Tn为数列{bn}的前n项和,
由Sn为数列{an}的前n项和,要证${S_n}>n-\frac{5}{2}$,
只需证n-Sn<$\frac{5}{2}$,即证Tn<$\frac{5}{2}$,
由bn+1=1-sin($\frac{π}{2}$(1-bn))=1-sin($\frac{π}{2}$-$\frac{π}{2}$bn)=1-cos$\frac{π}{2}$bn=2sin2$\frac{π}{4}$bn,
<2($\frac{π}{4}$bn)2≤$\frac{{π}^{2}}{16}$bn,
即Tn<$\frac{\frac{1}{2}}{1-\frac{{π}^{2}}{16}}$=$\frac{8}{{16-π}^{2}}$<1.305<$\frac{5}{2}$,
则${S_n}>n-\frac{5}{2}$成立;
(2)(Ⅰ)在数列{an}中,a1=1,${a}_{n+1}=c{a}_{n}{+c}^{n+1}(2n+1)$,n∈N*,
可得$\frac{{a}_{n+1}}{{c}^{n+1}}$=$\frac{{a}_{n}}{{c}^{n}}$+2n+1,
即有$\frac{{a}_{n}}{{c}^{n}}$=$\frac{{a}_{1}}{c}$+($\frac{{a}_{2}}{{c}^{2}}$-$\frac{{a}_{1}}{c}$)+($\frac{{a}_{3}}{{c}^{3}}$-$\frac{{a}_{2}}{{c}^{2}}$)+…+($\frac{{a}_{n}}{{c}^{n}}$-$\frac{{a}_{n-1}}{{c}^{n-1}}$)=$\frac{1}{c}$+3+5+…+2n-1=$\frac{1}{c}$+n2-1,
可得an=(n2-1)cn+cn-1,
(Ⅱ)由对一切k∈N*有a2k>a2k-1,可得
一切k∈N*有4(c2-c)k2+4ck-c2+c-1>0.
设f(x)=4(c2-c)x2+4cx-c2+c-1,对称轴为x=-$\frac{1}{2c-1}$,
由f(1)=3c2+c-1>0,可得c>$\frac{-1+\sqrt{13}}{6}$或c<$\frac{-1-\sqrt{13}}{6}$,
由c2-c≥0,即c≥1或c≤0,即有c≥1或c<$\frac{-1-\sqrt{13}}{6}$,
下面证c在这个范围内不等式恒成立.
当c≥1时,f(x)的对称轴为x=-$\frac{1}{2c-1}$<0,f(1)>0,得证x≥1时,f(x)>0成立;
当c<$\frac{-1-\sqrt{13}}{6}$时,f(x)的对称轴为x=-$\frac{1}{2c-1}$<$\frac{1}{2}$,可得f(x)在(1,+∞)递增,f(1)>0,
可得x≥1时,f(x)>0成立.
综上可得,c的范围是(-∞,$\frac{-1-\sqrt{13}}{6}$)∪[1,+∞).
点评 本题考查数列不等式的证明,注意运用分析法,结合正弦函数的图象和性质,考查数列通项公式的求法,注意运用数列恒等式,考查数列不等式恒成立问题解法,注意运用构造函数法,考查运算和推理能力,属于难题.


科目:高中数学 来源: 题型:解答题
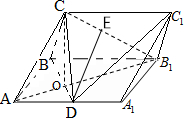 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=$\sqrt{2}$,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1,E为线段B1C的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=$\sqrt{2}$,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1,E为线段B1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x-y-5=0 | B. | x-3y+9=0 | C. | 3x+y-13=0 | D. | x+3y-15=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组别 | [65,75) | [75,85) | [85,95) | [95,105) | [105,115) | [115,150) |
| 频数 | 3 | 4 | 13 | 15 | 10 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 元朝时,著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,与店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的x=0,问一开始输入的x=( )
元朝时,著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,与店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的x=0,问一开始输入的x=( )| A. | $\frac{3}{4}$ | B. | $\frac{7}{8}$ | C. | $\frac{15}{16}$ | D. | $\frac{31}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(千万元) | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+b=22 | B. | a+b=21 | C. | ab=20 | D. | ab=21 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com