
【题目】已知函数h(x)=x2ex,f(x)=h(x)﹣aex(a∈R).
(Ⅰ)求函数h(x)的单调区间;
(Ⅱ)若x1,x2∈(1,2),且x1≠x2,使得f(x1)=f(x2)成立,求a的取值范围;
(Ⅲ)若函数f(x)有两个不同的极值点x1,x2,求证:f(x1)f(x2)<4e﹣2.
【答案】(Ⅰ)增区间是(﹣∞,﹣2),(0,+∞);减区间是(﹣2,0).(Ⅱ)(3,8).(Ⅲ)见解析
【解析】
(Ⅰ)求得函数的导数,根据函数f(x)导数的符号,然后确定原函数的单调性;
(Ⅱ)要满足题意,只需函数在(1,2)内有增有减,即存在极值点,则问题转化为函数的导数在(1,2)内存在变号根即可;
(Ⅲ)先求出f(x)的两个极值点,然后对两个极值点的函数值结合单调性作比较来证明结论.
(Ⅰ)h(x)=x2ex,∴h′(x)=ex(x2+2x),
当x∈(﹣∞,﹣2)∪(0,+∞)时,h′(x)>0,h(x)的增区间是(﹣∞,﹣2),(0,+∞);
当x∈(﹣2,0)时,h′(x)<0,所以h(x)的减区间是(﹣2,0).
(Ⅱ)依题意,函数f(x)=ex(x2﹣a)在(1,2)上不是单调函数,
因为f(x)是连续函数,所以f(x)在(1,2)上需有极值,
由于f′(x)=ex(x2+2x﹣a),即x2+2x﹣a=0在(1,2)内有变号根,
令u(x)=x2+2x﹣a,显然该函数在(1,2)上递增,
故需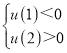 ,即
,即![]() ,解得3<a<8,
,解得3<a<8,
所以a的范围是(3,8).
(Ⅲ)由h(x)=x2ex,f(x)=h(x)﹣aex,则f(x)=x2ex﹣aex,
可得f′(x)=ex(x2+2x﹣a),
设方程ex(x2+2x﹣a)=0的两个不等实根是x1,x2,
则首先满足△=4+4a>0,解得a>﹣1,
又由x2+2x﹣a=0,解得,![]() ,此时x1+x2=﹣2,x1x2=﹣a.
,此时x1+x2=﹣2,x1x2=﹣a.
随着x的变化,f′(x),f(x)的变化如下:
x | (﹣∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
f′(x) | + | 0 | ﹣ | 0 | + |
f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
所以x1是函数f(x)的极大值点,x2是f(x)的极小值点.所以f(x1)是极大值,f(x2)是极小值,
![]()
![]()
![]() ,
,
又因为![]() ,所以
,所以![]()
所以![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ax+b,g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(1)求a,b,c,d的值;
(2)若x≥-2时,恒有f(x)≤kg(x),求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
![]()
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量![]() (单位:瓶)的分布列;
(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为![]() (单位:元),当六月份这种酸奶一天的进货量
(单位:元),当六月份这种酸奶一天的进货量![]() (单位:瓶)为多少时?
(单位:瓶)为多少时?![]() 的数学期望达到最大值?
的数学期望达到最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着国家二孩政策的全面放开,为了调查一线城市和非一线城市的二孩生育意愿,某机构用简单随机抽样方法从不同地区调查了![]() 位育龄妇女,结果如表.
位育龄妇女,结果如表.
非一线 | 一线 | 总计 | |
愿生 |
|
|
|
不愿生 |
|
|
|
总计 |
|
|
|
附表:
|
|
|
|
|
|
|
|
由![]() 算得,
算得,![]() 参照附表,得到的正确结论是( )
参照附表,得到的正确结论是( )
A. 在犯错误的概率不超过![]() 的前提下,认为“生育意愿与城市级别有关”
的前提下,认为“生育意愿与城市级别有关”
B. 有![]() 以上的把握认为“生育意愿与城市级别有关”
以上的把握认为“生育意愿与城市级别有关”
C. 在犯错误的概率不超过![]() 的前提下,认为“生育意愿与城市级别无关”
的前提下,认为“生育意愿与城市级别无关”
D. 有![]() 以上的把握认为“生育意愿与城市级别无关”
以上的把握认为“生育意愿与城市级别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两人进行定点投篮活动,已知他们每投篮一次投中的概率分别是![]() 和
和![]() ,每次投篮相互独立互不影响.
,每次投篮相互独立互不影响.
(Ⅰ)甲乙各投篮一次,记“至少有一人投中”为事件A,求事件A发生的概率;
(Ⅱ)甲乙各投篮一次,记两人投中次数的和为X,求随机变量X的分布列及数学期望;
(Ⅲ)甲投篮5次,投中次数为ξ,求ξ=2的概率和随机变量ξ的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年“双十一”期间,某商场举办了一次有奖促销活动,顾客消费每满1000元可参加一次抽奖(例如:顾客甲消费930元,不得参与抽奖;顾客乙消费3400元,可以抽奖三次)。如图1,在圆盘上绘制了标有A,B,C,D的八个扇形区域,每次抽奖时由顾客按动按钮使指针旋转一次,旋转结束时指针会随机停在圆盘上的某一个位置,顾客获奖的奖次由指针所指区域决定(指针与区域边界线粗细忽略不计)。商家规定:指针停在标A,B,C,D的扇形区域分别对应的奖金为200元、150元、100元和50元。已知标有A,B,C,D的扇形区域的圆心角成等差数列,且标D的扇形区域的圆心角是标A的扇形区域的圆心角的4倍.
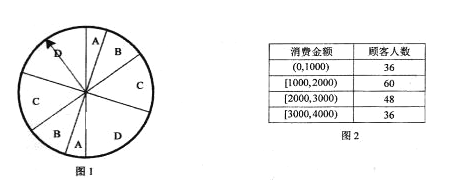
(I)某顾客只抽奖一次,设该顾客抽奖所获得的奖金数为X元,求X的分布列和数学期望;
(II)如图2,该商场统计了活动期间一天的顾客消费情况.现按照消费金额分层抽样选出15位顾客代表,其中获得奖金总数不足100元的顾客代表有7位.现从这7位顾客代表中随机选取两位,求这两位顾客的奖金总数和仍不足100元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2011年,国际数学协会正式宣布,将每年的3月14日设为“国际数学节”,其来源是中国古代数学家祖冲之的圆周率,为庆祝该节日,某校举办的“数学嘉年华”活动中,设计了如下的有奖闯关游戏:参赛选手按第一关、第二关、第三关的顺序依次闯关,若闯关成功,则分别获得5个、10个、20个学豆的奖励.游戏还规定:当选手闯过一关后,可以选择带走相应的学豆,结束游戏;也可以选择继续闯下一关,若有任何一关没有闯关成功,则全部学豆归零,游戏结束.设选手甲能闯过第一关、第二关、第三关的概率分别为![]() ,选手选择继续闯关的概率均为
,选手选择继续闯关的概率均为![]() ,且各关之间闯关成功与否互不影响.
,且各关之间闯关成功与否互不影响.
(1)求选手甲第一关闯关成功且所得学豆为零的概率;
(2)设该选手所得学豆总数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆锥![]() (其中
(其中![]() 为顶点,
为顶点,![]() 为底面圆心)的侧面积与底面积的比是
为底面圆心)的侧面积与底面积的比是![]() ,则圆锥
,则圆锥![]() 与它外接球(即顶点在球面上且底面圆周也在球面上)的体积比为( )
与它外接球(即顶点在球面上且底面圆周也在球面上)的体积比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,国内很多评价机构经过反复调研论证,研制出“增值评价”方式。下面实例是某市对“增值评价”的简单应用,该市教育评价部门对本市![]() 所高中按照分层抽样的方式抽出
所高中按照分层抽样的方式抽出![]() 所(其中,“重点高中”
所(其中,“重点高中”![]() 所分别记为
所分别记为![]() ,“普通高中”
,“普通高中”![]() 所分别记为
所分别记为![]() ),进行跟踪统计分析,将
),进行跟踪统计分析,将![]() 所高中新生进行了统的入学测试高考后,该市教育评价部门将人学测试成绩与高考成绩的各校平均总分绘制成了雷达图.
所高中新生进行了统的入学测试高考后,该市教育评价部门将人学测试成绩与高考成绩的各校平均总分绘制成了雷达图.![]() 点表示
点表示![]() 学校入学测试平均总分大约
学校入学测试平均总分大约![]() 分,
分,![]() 点表示
点表示![]() 学校高考平均总分大约
学校高考平均总分大约![]() 分,则下列叙述不正确的是( )
分,则下列叙述不正确的是( )

A.各校人学统一测试的成绩都在![]() 分以上
分以上
B.高考平均总分超过![]() 分的学校有
分的学校有![]() 所
所
C.![]() 学校成绩出现负增幅现象
学校成绩出现负增幅现象
D.“普通高中”学生成绩上升比较明显
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com