已知P,A,B,C是以O为球心的球面上的四个点,PA,PB,PC两两垂直,且PA=PB=PC=2,则球O的半径为 ;球心O到平面ABC的距离为 .
【答案】
分析:PA、PB、PC可看作是正方体的一个顶点发出的三条棱,所以过空间四个点P、A、B、C的球面即为棱长为2的正方体的外接球,球的直径即是正方体的对角线,求出对角线长,即可求出球的半径,而球心O到平面ABC的距离为体对角线的

.
解答:解:空间四个点P、A、B、C在同一球面上,PA、PB、PC两两垂直,且PA=PB=PC=a,则PA、PB、PC可看作是正方体的一个顶点发出的三条棱,所以过空间四个点P、A、B、C的球面即为棱长为2的正方体的外接球,球的直径即是正方体的对角线,长为 2
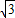
,所以这个球面的半径
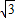
,球心O到平面ABC的距离为体对角线的

,即球心O到平面ABC的距离为
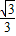
.
故答案为:
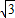
;
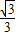 点评:
点评:本题是基础题,考查球的内接体知识,球的表面积的求法,考查空间想象能力,计算能力,分析出,正方体的对角线就是球的直径是解好本题的关键所在.

 .
.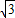 ,所以这个球面的半径
,所以这个球面的半径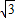 ,球心O到平面ABC的距离为体对角线的
,球心O到平面ABC的距离为体对角线的 ,即球心O到平面ABC的距离为
,即球心O到平面ABC的距离为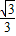 .
.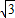 ;
;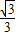


 阅读快车系列答案
阅读快车系列答案