Question

20．一个四棱锥的三视图和直观图如图所示，E为侧棱PD的中点．
（1）求证：PB∥平面AEC；
（2）求三棱锥C-PAB的体积．
（3）若F为侧棱PA上一点，且$\frac{PF}{FA}$=λ，则λ为何值时，PA⊥平面BDF．

Answer 1

分析 （1）设AC、BD的交点为O，连接OE，由三角形的中位线定理可得，OE∥PB，再由线面平行的判定定理，即可得到PB∥平面AEC；
（2）连接OP，则OP⊥平面ABCD，由V_C-PAB=V_P-ABC，利用等体积法能求出三棱锥C-PAB的体积．
（3）以O为原点，OB为x轴，OC为y轴，OP为z轴，建立空间直角坐标系，利用向量法能求出λ=3时，PA⊥平面BDF．

解答 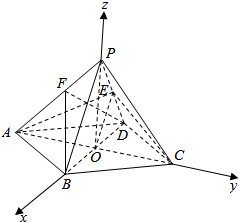解：（1）由已知中俯视图可知该几何体为底面ABCD为菱形，且有一个角为60°，边长为2，
由正视图和侧视图可得：几何体为高度为PO=3的四棱锥，
设AC、BD的交点为O，连接OE，
∵E为侧棱PD的中点，∴OE为△DPB的中位线，∴OE∥PB，
又由OE?平面EAC，PB?平面EAC，
∴PB∥平面AEC．
（2）连接OP，则OP⊥平面ABCD
由OP=3，底面ABCD为菱形，且有一个角为60°，边长为2，
则OD=1，AC=2$\sqrt{3}$，PB=PD=$\sqrt{10}$，PA=PC=2$\sqrt{3}$，
S_△ABC=$\frac{1}{2}AC×OB$=$\frac{1}{2}×2\sqrt{3}×1$=$\sqrt{3}$，
∴三棱锥C-PAB的体积：
V_C-PAB=V_P-ABC=$\frac{1}{3}{S}_{△ABC}×OP$=$\frac{1}{3}×\sqrt{3}×3=\sqrt{3}$．
（3）以O为原点，OB为x轴，OC为y轴，OP为z轴，建立空间直角坐标系，
P（0，0，3），A（0，-$\sqrt{3}$，0），B（1，0，0），D（-1，0，0），
设F（0，b，c），∵$\frac{PF}{FA}$=λ，∴$\overrightarrow{PF}=λ\overrightarrow{FA}$，
∴$（0，b，c-3）=λ（0，-\sqrt{3}-b，-c）$，∴$\left\{\begin{array}{l}{b=-\sqrt{3}λ-bλ}\\{c-3=-cλ}\end{array}\right.$，∴$\left\{\begin{array}{l}{b=-\frac{\sqrt{3}λ}{λ+1}}\\{c=\frac{3}{1+λ}}\end{array}\right.$，
∴$\overrightarrow{BF}$=（-1，-$\frac{\sqrt{3}λ}{λ+1}$，$\frac{3}{1+λ}$），$\overrightarrow{DF}$=（1，-$\frac{\sqrt{3}λ}{λ+1}$，$\frac{3}{1+λ}$），$\overrightarrow{PA}$=（0，-$\sqrt{3}$，-3），
∵PA⊥平面BDF，∴（-$\frac{\sqrt{3}λ}{λ+1}$）（-$\sqrt{3}$）+$\frac{3}{1+λ}×（-3）$=0，
解得λ=3．
∴λ=3时，PA⊥平面BDF．

点评 本题考查的知识点是直线与平面平行的判定，棱锥体积的求法，直线与平面垂直的判定，是中档题，解题时要认真审题，注意向量法的合理运用．