
(本题满分12分)设椭圆C:![]() (“a>b〉0)的左焦点为
(“a>b〉0)的左焦点为![]() ,椭圆过点P(
,椭圆过点P(![]() ).(1)求椭圆C的方程;
).(1)求椭圆C的方程;
(2)已知点D(1, 0),直线l:![]() 与椭圆C交于a、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围.
与椭圆C交于a、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围.
解 (1)由题意知![]() ,b2 = a2-3,由
,b2 = a2-3,由 得 2a4-11a2 + 12 = 0,
得 2a4-11a2 + 12 = 0,
所以(a2-4)(2a2-3)= 0,得 a2 = 4或![]() (舍去),
(舍去),
因此椭圆C的方程为![]() . ……………… 4分
. ……………… 4分
(2)由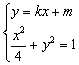 得
得 ![]() .
.
所以4k2 + 1>0,![]() ,
,
得 4k2 + 1>m2. ① ……………… 6分
设A(x1,y1),B(x2,y2),AB中点为M(x0,y0),则![]() ,
,![]() ,
,
于是 ![]() ,
,![]() ,
,![]() .
.
设菱形一条对角线的方程为![]() ,则有 x =-ky + 1.
,则有 x =-ky + 1.
将点M的坐标代入,得 ![]() ,所以
,所以![]() . ②
. ②
……………… 9分
将②代入①,得![]() ,
,
所以9k2>4k2 + 1,解得 k∈![]() . ……………… 12分
. ……………… 12分
法2 ![]()
![]() .直线l的方向向量为(1,k),则由菱形对角线互相垂直得
.直线l的方向向量为(1,k),则由菱形对角线互相垂直得![]() ,即
,即![]() ,-3km = 4k2 + 1,
,-3km = 4k2 + 1,![]() , 代入①即得.
, 代入①即得.
法3 设A(x1,y1),B(x2,y2),AB中点为M(x0,y0),则![]() ,
,![]() ,
,
于是,两式相减可得 ![]() ,即 x0 + 4ky0 = 0. ①
,即 x0 + 4ky0 = 0. ①
因为 QD⊥AB,所以 ![]() . ②
. ②
由①②可解得 ![]() ,
,![]() ,表明点M的轨迹为线段
,表明点M的轨迹为线段![]() (
(![]() ).
).
当![]() ,k∈(
,k∈(![]() ,+∞);当
,+∞);当![]() ,k∈(-∞,
,k∈(-∞,![]() ).
).
综上,k的取值范围是k∈![]() .
.


科目:高中数学 来源:2014届吉林省吉林市高二上学期期中理科数学试卷(解析版) 题型:解答题
(本题满分12分)
设命题 :实数
:实数 满足
满足 , 命题
, 命题 :实数
:实数 满足
满足 .
.
当 为真,求实数
为真,求实数 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省石家庄市高三暑期第二次考试理科数学试卷(解析版) 题型:解答题
(本题满分12分)设函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省高三十一月份阶段性考试理科数学 题型:解答题
(本题满分12分)设函数 ,其中
,其中 。
。
(Ⅰ)当 时,求不等式
时,求不等式 的解集;
的解集;
(Ⅱ)若不等式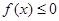 的解集为
的解集为 ,求a的值。
,求a的值。
查看答案和解析>>
科目:高中数学 来源:2010-2011年云南省高二上学期期末数学理卷 题型:解答题
(本题满分12分)
设 ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 斜率为1的直线
斜率为1的直线 与
与 相交于
相交于 、
、 两点,且
两点,且 ,
, ,
, 成等差数列,
成等差数列,
(Ⅰ)求 的离心率;
的离心率;
(Ⅱ)设点 满足
满足 ,求
,求 的方程。
的方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com