
已知椭圆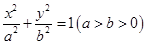 的左右两焦点分别为
的左右两焦点分别为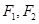 ,
, 是椭圆上一点,且在
是椭圆上一点,且在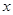 轴上方,
轴上方,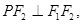
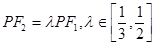 .
.
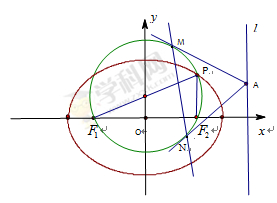
(1)求椭圆的离心率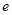 的取值范围;
的取值范围;
(2)当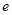 取最大值时,过
取最大值时,过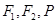 的圆
的圆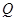 的截
的截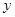 轴的线段长为6,求椭圆的方程;
轴的线段长为6,求椭圆的方程;
(3)在(2)的条件下,过椭圆右准线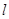 上任一点
上任一点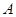 引圆
引圆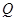 的两条切线,切点分别为
的两条切线,切点分别为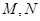 .试探究直线
.试探究直线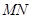 是否过定点?若过定点,请求出该定点;否则,请说明理由.
是否过定点?若过定点,请求出该定点;否则,请说明理由.
(1)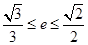 ;(2)
;(2)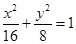 ;(3)
;(3)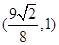 .
.
【解析】
试题分析:(1)由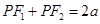 ,
, ,
,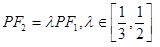 .即可求得
.即可求得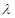 的取值范围.
的取值范围.
(2)由(1)可得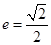 .以及
.以及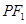 是圆的直径可得
是圆的直径可得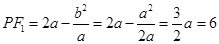 .即可求出椭圆的方程.
.即可求出椭圆的方程.
(3)由(2)可得圆Q的方程.切点M,N所在的圆的方程上任一点坐标为P(x,y).由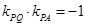 .即得
.即得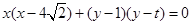 .则M,N所在的直线方程为.两圆方程对减即可得到.根据过定点的知识即可求出定点.本题涉及的知识点较多,渗透方程的思想,加强对几何图形的关系理解.
.则M,N所在的直线方程为.两圆方程对减即可得到.根据过定点的知识即可求出定点.本题涉及的知识点较多,渗透方程的思想,加强对几何图形的关系理解.
试题解析: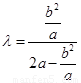 , ∴
, ∴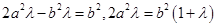 ,
,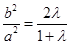 .
.
(1)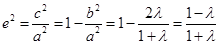 ,∴
,∴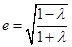 ,在
,在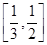 上单调递减.
上单调递减.
∴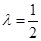 时,
时,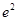 最小
最小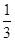 ,
,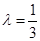 时,
时,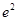 最大
最大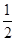 ,∴
,∴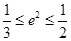 ,∴
,∴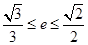 .
.
(2)当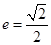 时,
时,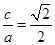 ,∴
,∴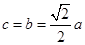 ,∴
,∴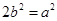 .
.
∵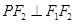 ,∴
,∴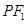 是圆的直径,圆心是
是圆的直径,圆心是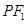 的中点,∴在y轴上截得的弦长就是直径,∴
的中点,∴在y轴上截得的弦长就是直径,∴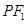 =6.又
=6.又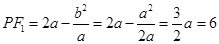 ,∴
,∴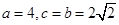 .∴椭圆方程是
.∴椭圆方程是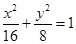 10分
10分
(3)由(2)得到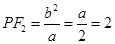 ,于是圆心
,于是圆心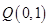 ,半径为3,圆
,半径为3,圆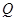 的方程是
的方程是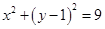 .椭圆的右准线方程为
.椭圆的右准线方程为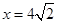 ,,∵直线AM,AN是圆Q的两条切线,∴切点M,N在以AQ为直径的圆上.设A点坐标为
,,∵直线AM,AN是圆Q的两条切线,∴切点M,N在以AQ为直径的圆上.设A点坐标为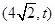 ,∴该圆方程为
,∴该圆方程为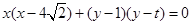 .∴直线MN是两圆的公共弦,两圆方程相减得:
.∴直线MN是两圆的公共弦,两圆方程相减得: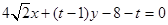 ,这就是直线MN的方程.该直线化为:
,这就是直线MN的方程.该直线化为: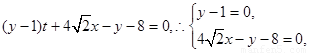
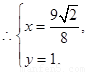
∴直线MN必过定点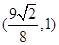 .
16分
.
16分
考点:1.椭圆的离心率.2.椭圆的标准方程.3.两圆的公共线的方程.4.过定点问题.


科目:高中数学 来源: 题型:解答题
 的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点,若
的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点,若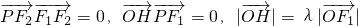 ,
,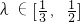 (其中O为坐标原点).求椭圆C离心率e的最大值.
(其中O为坐标原点).求椭圆C离心率e的最大值.查看答案和解析>>
科目:高中数学 来源:江苏模拟题 题型:解答题
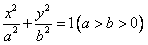 的左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,OH=λOF1,λ∈[
的左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,OH=λOF1,λ∈[ ,
, ]。
]。
查看答案和解析>>
科目:高中数学 来源:2010年陕西省咸阳市礼泉一中高三5月最后一次预测数学试卷(解析版) 题型:解答题
 的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点,若
的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点,若 ,
, (其中O为坐标原点).
(其中O为坐标原点). ,求直线l的方程.
,求直线l的方程.查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省苏州中学高三数学能力基础训练试卷2(解析版) 题型:解答题
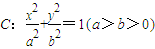 的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点,若
的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点,若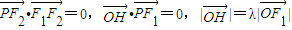 ,
,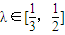 (其中O为坐标原点).求椭圆C离心率e的最大值.
(其中O为坐标原点).求椭圆C离心率e的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com