
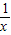 ,③对函数f(x)=|x2-2ax+b|配方,确定二次函数y=x2-2ax+b的最小值的符号,从而确定函数f(x)的单调性;④用min{a,b,c}表示a,b,c三个实数中的最小值,在同一坐标系中画出它们的图象,则可知函数f(x)的最大值.
,③对函数f(x)=|x2-2ax+b|配方,确定二次函数y=x2-2ax+b的最小值的符号,从而确定函数f(x)的单调性;④用min{a,b,c}表示a,b,c三个实数中的最小值,在同一坐标系中画出它们的图象,则可知函数f(x)的最大值.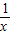 ,是奇函数,但是图象不过原点,也是幂函数,在(-∞,0)和(0,+∞)上是减函数;
,是奇函数,但是图象不过原点,也是幂函数,在(-∞,0)和(0,+∞)上是减函数; ③f(x)=|x2-2ax+b|=|(x-a)2+b-a2|
③f(x)=|x2-2ax+b|=|(x-a)2+b-a2|

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2014届湖南省高一12月月考数学 题型:填空题
下列四种说法中,其中正确的是 (将你认为正确的序号都填上)
①奇函数的图像必经过原点;
②若幂函数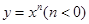 是奇函数,则
是奇函数,则 在定义域内为减函数;
在定义域内为减函数;
③函数 ,若
,若 ,则
,则 在区间
在区间 上是增函数;
上是增函数;
④用 表示
表示 三个实数中的最小值,设
三个实数中的最小值,设 ,则函数
,则函数 的最大值为6。
的最大值为6。
查看答案和解析>>
科目:高中数学 来源:2014届湖南省高一12月月考数学 题型:填空题
下列四种说法中,其中正确的是 (将你认为正确的序号都填上)
①奇函数的图像必经过原点;
②若幂函数 是奇函数,则
是奇函数,则 在定义域内为减函数;
在定义域内为减函数;
③函数 ,若
,若 ,则
,则 在区间
在区间 上是增函数;
上是增函数;
④用 表示
表示 三个实数中的最小值,设
三个实数中的最小值,设 ,则函数
,则函数 的最大值为6。
的最大值为6。
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com