
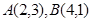 ,直线
,直线 ,在直线
,在直线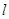 上求一点
上求一点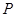 .
.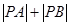 最小; (2)使
最小; (2)使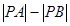 最大.
最大. 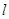 的交点可求得为
的交点可求得为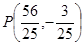 ,由平面几何知识可知
,由平面几何知识可知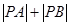 最小.(2)直线AB与
最小.(2)直线AB与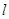 的交点可求得为
的交点可求得为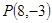 ,它使
,它使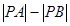 最大.
最大.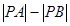 的最大值,则利用两点在直线的同侧,可以连线,延长与直线相交,结合两边之差小于等于第三边,当三点共线的时候满足最大值得到结论。
的最大值,则利用两点在直线的同侧,可以连线,延长与直线相交,结合两边之差小于等于第三边,当三点共线的时候满足最大值得到结论。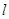 的对称点A1的坐标为(x1,y1).
的对称点A1的坐标为(x1,y1).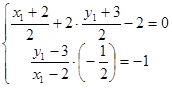 ﹍﹍﹍﹍﹍2分
﹍﹍﹍﹍﹍2分 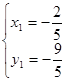 ﹍﹍﹍﹍4分
﹍﹍﹍﹍4分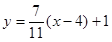 , ﹍﹍﹍﹍5分
, ﹍﹍﹍﹍5分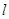 的交点可求得为
的交点可求得为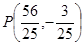 ﹍﹍﹍﹍6分
﹍﹍﹍﹍6分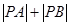 最小.
最小.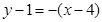 ,即
,即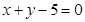 .﹍﹍﹍﹍8分
.﹍﹍﹍﹍8分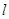 的交点可求得为
的交点可求得为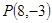 ,它使
,它使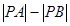 最大. ﹍﹍﹍﹍12分
最大. ﹍﹍﹍﹍12分

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com