
 +
+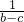 恒成立时,λ的最大值为________.
恒成立时,λ的最大值为________. +
+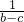 的最小值,又实数λ≤
的最小值,又实数λ≤ +
+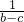 恒成立时,λ≤
恒成立时,λ≤ +
+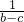 的最小值,分析可得λ的最大值,即可得答案.
的最小值,分析可得λ的最大值,即可得答案.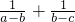 =(a-b)+(b-c)+
=(a-b)+(b-c)+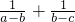 -2≥2,
-2≥2,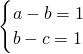 时等号成立)
时等号成立) +
+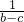 恒成立时,λ≤2,
恒成立时,λ≤2,

 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
 如图,在平面直坐标系xOy中,已知椭圆C:
如图,在平面直坐标系xOy中,已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
如图为测量两山顶C、D的距离,直升机沿水平方向在A、B两点进行测量,A、B、C、D在同一铅直平面内,在A处测得C、D均在前方,俯角分别为![]() 和
和![]() ,在B处测得C在前方,D在后方,且D处俯角为
,在B处测得C在前方,D在后方,且D处俯角为![]() ,
,![]() 为
为![]() ,已知
,已知![]()
![]() ,
,![]() ,求C、D的距离(结果用根式表示)
,求C、D的距离(结果用根式表示)

查看答案和解析>>
科目:高中数学 来源:2011-2012学年云南省昆明一中高三(上)第二次摸底数学试卷(文科)(解析版) 题型:选择题
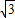 ,若球O的体积为
,若球O的体积为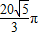 ,则这个直三棱柱的体积等于( )
,则这个直三棱柱的体积等于( )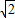
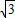
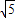
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com