

 ,
, ,从而可求平面PMN与水平面所成角的余弦值;
,从而可求平面PMN与水平面所成角的余弦值; ,水平面PAB的一个法向量
,水平面PAB的一个法向量 ,利用向量的夹角公式,即可求得平面PMN与水平面所成角的余弦值;
,利用向量的夹角公式,即可求得平面PMN与水平面所成角的余弦值; ,从而可得平面PMN与水平面所成角的余弦值.
,从而可得平面PMN与水平面所成角的余弦值.
 米
米 


 ,
,



 ,则
,则
 令x=1,解得
令x=1,解得
 ,
, =
= ,
, .
. 得
得 ,
, ,
,
 .
.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 在抗震救灾行动中,某部队在如图所示的P处空降了一批救灾药品,急需把这批药品沿道路PA,PB送到矩形灾民区ABCD中去,已知PA=100km,PB=150km,BC=60km,∠APB=60°,试在灾民区确定一条界线,使位于界线一侧的点沿道路PA送药较近,而另一侧的点沿道路PB送药较近,请说明这一界线是一条什么曲线?并求出其方程.
在抗震救灾行动中,某部队在如图所示的P处空降了一批救灾药品,急需把这批药品沿道路PA,PB送到矩形灾民区ABCD中去,已知PA=100km,PB=150km,BC=60km,∠APB=60°,试在灾民区确定一条界线,使位于界线一侧的点沿道路PA送药较近,而另一侧的点沿道路PB送药较近,请说明这一界线是一条什么曲线?并求出其方程.查看答案和解析>>
科目:高中数学 来源: 题型:
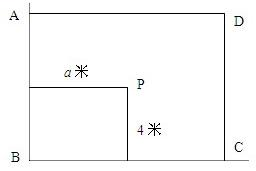
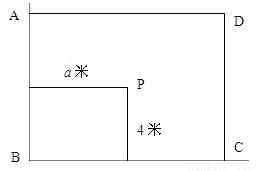
 如图,从山脚下P处经过山腰N到山顶M拉一条电缆,PN的长为a米,NM的长为2a米,在P处测得M、N的仰角分别为45°,30°,在N处测得M的仰角为30°.
如图,从山脚下P处经过山腰N到山顶M拉一条电缆,PN的长为a米,NM的长为2a米,在P处测得M、N的仰角分别为45°,30°,在N处测得M的仰角为30°.查看答案和解析>>
科目:高中数学 来源:2011年高三数学第一轮基础知识训练(32)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com