Question

甲、乙、丙三名射击运动员射中目标的概率分别为，a，a(0<a<1)，三人各射击一次，击中目标的次数记为ξ.

(1)求ξ的分布列及数学期望；

(2)在概率P(ξ＝i)(i＝0,1,2,3)中，若P(ξ＝1)的值最大， 求实数a的取值范围.

Answer 1

 (1)由题意ξ的可能取值为0,1,2,3.

P(ξ＝0)＝×(1－) (1－a)²＝(1－a)²，

P(ξ＝1)＝× (1－a)²＋×(1－)a(1－a)＝(1－a²)，

P(ξ＝2)＝×a(1－a)＋×(1－)a²

＝(2a－a²)，

P(ξ＝3)＝×a²＝.

所以ξ的分布列为

ξ	0	1	2	3
P	(1－a)2	(1－a2)	(2a－a2)

ξ的数学期望为

E(ξ)＝0×(1－a)²＋1×(1－a²)＋2×(2a－a²)＋3×＝＋2a.

(2)P(ξ＝1)－P(ξ＝0)＝[(1－a²)－(1－a)²]＝a(1－a)，

P(ξ＝1)－P(ξ＝2)＝[(1－a²)－(2a－a²)]＝，

P(ξ＝1)－P(ξ＝3)＝[(1－a²)－a²]＝，

由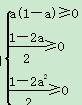和0<a<1，得0<a≤，

即a的取值范围是(0，].