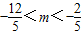【答案】
分析:由已知中圆C
1:x
2+y
2-2mx+m
2=4和C
2:x
2+y
2+2x-4my=8-4m
2的一般方程,我们可以求出两个圆的圆心坐标和半径,进而求出圆心距,根据两圆相交,则|r
1-r
2|≤d≤r
1+r
2,我们可以构造出关于m的不等式组,解不等式组,即可求出m的取值范围.
解答:解:∵圆C
1:x
2+y
2-2mx+m
2=4的圆心坐标C
1(m,0),半径r
1=2,
圆C
2:x
2+y
2+2x-4my=8-4m
2的圆心坐标C
2(-1,2m),半径r
2=3,
则圆心距d=|C
1C
2|=
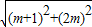
=
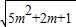
若圆C
1:x
2+y
2-2mx+m
2=4和C
2:x
2+y
2+2x-4my=8-4m
2相交,
则|r
1-r
2|≤d≤r
1+r
2,
即1≤
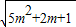
≤5
解得0<m<2或
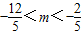
故选D
点评:本题考查的知识点是圆与圆的位置关系,两点之间的距离公式,其中熟练掌握圆与圆位置关系的判定方法,根据已知中两圆相交,转化得到|r
1-r
2|≤d≤r
1+r
2,是解答本题的关键.



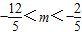
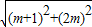 =
=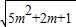
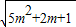 ≤5
≤5