
(1)求轨迹E的方程;
(2)若直线l过点F2且与轨迹E交于P、Q两点.
①无论直线l绕点F2怎样转动,在x轴上总存在定点M(m,0),使MP⊥MQ恒成立,求实数m的值.
②过P、Q作直线x=![]() 的垂线PA、QB,垂足分别为A、B,记λ=
的垂线PA、QB,垂足分别为A、B,记λ=![]() ,求λ的取值范围.
,求λ的取值范围.
(文)已知等差数列{an}中,a1=-2,a2=1.
(1)求{an}的通项公式;
(2)调整数列{an}的前三项a1、a2、a3的顺序,使它成为等比数列{bn}的前三项,求{bn}的前n项和.
答案:(理)解:(1)由|PF1|-|PF2|=2<|F1F2|,知点P的轨迹E是以F1、F2为焦点的双曲线右支,由c=2,2a=2,∴b2=3.故轨迹E的方程为x2![]() =1(x≥1).
=1(x≥1).
(2)当直线l的斜率存在时,设直线方程为y=k(x-2),P(x1,y1),Q(x2,y2),与双曲线方程联立消去y,得(k2-3)x2-4k2x+4k2+3=0.
∴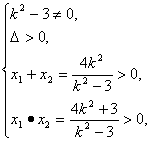
①∵![]() =(x1-m)(x2-m)+y1y2=(x1-m)(x2-m)+k2(x1-2)(x2-2)
=(x1-m)(x2-m)+y1y2=(x1-m)(x2-m)+k2(x1-2)(x2-2)
=(k2+1)x1x2-(2k2+m)(x1+x2)+m2+4k2
=![]() =
=![]() +m2.
+m2.
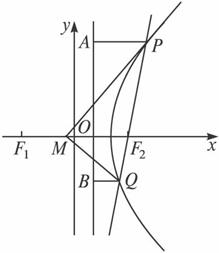
∵MP⊥MQ,∴![]() =0.故得3(1-m2)+k2(m2-4m-5)=0对任意的k2>3恒成立,
=0.故得3(1-m2)+k2(m2-4m-5)=0对任意的k2>3恒成立,
∴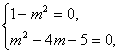 解得m=-1.∴当m=-1时,MP⊥MQ.
解得m=-1.∴当m=-1时,MP⊥MQ.
当直线l的斜率不存在时,由P(2,3),Q(2,-3)及M(-1,0),知结论也成立,综上,当m=-1时,MP⊥MQ.
②∵a=1,c=2,

∴直线x=![]() 是双曲线的右准线.由双曲线定义,得|PA|=
是双曲线的右准线.由双曲线定义,得|PA|=![]() |PF2|=
|PF2|=![]() |PF2|,|QB|=
|PF2|,|QB|=![]() |QF2|.
|QF2|.
∴λ=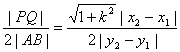 =
=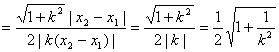 .
.
∵k2>3,∴0<![]() <
<![]() ,故
,故![]() <λ<
<λ<![]() .
.
注意到直线的斜率不存在时,|PQ|=|AB|,此时λ=![]() .综上,λ=[
.综上,λ=[![]() ,
,![]() ).
).
(文)解:(1)由已知,得a2-a1=1-(-2)=3,∴{an}的公差d=3.∴an=a1+(n-1)d=-2+3(n-1)=3n-5.
(2)由(1)得a3=a2+d=1+3=4,∴a1=-2,a2=1,a3=4.依题意,可得数列{bn}的前三项为b1=1,b2=-2,b3=4或b1=4,b2=-2,b3=1.
①当数列{bn}的前三项为b1=1,b2=-2,b3=4时,则q=-2,
∴Sn=![]() =
=![]() [1-(-2)n].
[1-(-2)n].
②当数列{bn}的前三项为b1=4,b2=-2,b3=1时,则q=-![]() .
.
∴Sn=![]()
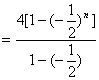 =
=![]() [1-(-
[1-(-![]() )n].
)n].


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 2 |
| 2 |
| TF1 |
| TF2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年南昌市一模理)(12分)已知F1、F2是椭圆![]() 的两个焦点,O为坐标原点,点P
的两个焦点,O为坐标原点,点P![]() )在椭圆上,线段PF2与y轴的交点M满足
)在椭圆上,线段PF2与y轴的交点M满足![]() ;⊙O是以F1F2为直径的圆,一直线l: y=kx+m与⊙O相切,并与椭圆交于不同的两点A、B.
;⊙O是以F1F2为直径的圆,一直线l: y=kx+m与⊙O相切,并与椭圆交于不同的两点A、B.
(1)求椭圆的标准方程;
(2)当![]() ,且满足
,且满足![]() 时,求△AOB面积S的取值范围.
时,求△AOB面积S的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年赤峰二中模拟理) 已知F1(- 2, 0), F2 (2, 0), 点P满足| PF1| - | PF2| = 2, 记点P的轨迹为E.
(Ⅰ) 求轨迹E的方程;
(Ⅱ) 若直线l过点F2且与轨迹E交于P、Q两点,
①无论直线l绕点F2怎样转动, 在x轴上总存在定点M(m, 0), 使MP ^ MQ恒成立, 求实数m的值;
②过P、Q作直线x =![]() 的垂线PA、QB, 垂足分别为A、B, 记l =
的垂线PA、QB, 垂足分别为A、B, 记l =![]() , 求l的取值范围.
, 求l的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年赤峰二中模拟理) 已知f1(x) = sinx + cosx, f2(x) = f1¢(x), f3(x) = f2¢(x), ¼, fn(x) = f n - 1¢(x) (n Î N且 n ³ 2), 其中f ¢(x)是f (x)的导函数, 则f1(![]() ) + f2(
) + f2(![]() ) + ¼ + f2008(
) + ¼ + f2008(![]() ) = .
) = .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com