
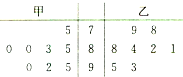
 (2012•开封一模)甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,用茎叶图表示这两组数据.
(2012•开封一模)甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,用茎叶图表示这两组数据.. |
| x甲 |
. |
| x乙 |
| 6 |
| 8 |
| 3 |
| 4 |
. |
| x乙 |
| 93+95+81+82+84+88+78+79 |
| 8 |
. |
| x甲 |
| 90+92+95+80+80+83+85+75 |
| 8 |
| 6 |
| 8 |
| 3 |
| 4 |
| 3 |
| 4 |
| C | k 3 |
| 3 |
| 4 |
| 1 |
| 4 |
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 64 |
| 9 |
| 64 |
| 27 |
| 64 |
| 27 |
| 64 |
| 9 |
| 4 |


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 5 |
| y2 |
| 4 |
| x2 |
| 5 |
| y2 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com