
(09 年石景山区统一测试理)(14分)
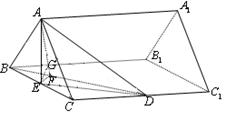
如图,已知正三棱柱![]() ―
―![]() 的底面边长是
的底面边长是![]() ,
,![]() 是侧棱
是侧棱![]() 的中点,直线
的中点,直线![]()
与侧面![]() 所成的角为
所成的角为![]() .
.
(Ⅰ)求此正三棱柱的侧棱长;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)求点![]() 到平面
到平面![]() 的距离.
的距离.

解析:解法一:
(Ⅰ)设正三棱柱![]() ―
―![]() 的侧棱长为
的侧棱长为![]() .取
.取![]() 中点
中点![]() ,连结
,连结![]() .
.
∵ ![]() 是正三角形,∴
是正三角形,∴ ![]() .
.
又底面![]() 侧面
侧面![]() ,
,
且两平面交线为![]() ,
,
∴ ![]() 侧面
侧面![]() .
.
连结![]() ,则
,则![]() 为直线
为直线![]() 与侧面
与侧面![]() 所成的角.
所成的角.
∴ ![]() . ………………2分
. ………………2分
在![]() 中,
中, ,解得
,解得![]() .
.
∴ 此正三棱柱的侧棱长为![]() . ………………4分
. ………………4分
(Ⅱ)过![]() 作
作![]() 于
于![]() ,连结
,连结![]() .
.
∵ ![]() 侧面
侧面![]() ,∴
,∴ ![]() 是
是![]() 在平面
在平面![]() 内的射影.
内的射影.
由三垂线定理,可知![]() .
.
∴ ![]() 为二面角
为二面角![]() 的平面角. ………………6分
的平面角. ………………6分
在![]() 中,
中,![]() ,又
,又![]() ,
,
 , ∴
, ∴ ![]() .
.
又![]() ,
,
∴ 在![]() 中,
中,![]() . ………………8分
. ………………8分
故二面角![]() 的大小为
的大小为![]() . ………………9分
. ………………9分
(Ⅲ)由(Ⅱ)可知,![]() 平面
平面![]() ,
,
∴ 平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,
,
过![]() 作
作![]() 于
于![]() ,则
,则![]() 平面
平面![]() .
.
∴ ![]() 的长为点
的长为点![]() 到平面
到平面![]() 的距离. ………………10分
的距离. ………………10分
在![]() 中,
中, . …………12分
. …………12分
∵ ![]() 为
为![]() 中点,∴ 点
中点,∴ 点![]() 到平面
到平面![]() 的距离为
的距离为![]() . …………14分
. …………14分
解法二:
(Ⅰ)同解法一.
(Ⅱ)如图,建立空间直角坐标系![]() .
.

则![]() .
.
设![]()
![]() 为平面
为平面![]() 的法向量.
的法向量.
由 ,
,
得 .
.
取![]() . …………6分
. …………6分
又平面![]() 的一个法向量
的一个法向量![]() . …………7分
. …………7分
∴  . …………8分
. …………8分
结合图形可知,二面角![]() 的大小为
的大小为![]() . …………9分
. …………9分
(Ⅲ)由(Ⅱ),![]() ,
,![]() . …………10分
. …………10分
∴ 点![]() 到平面
到平面![]() 的距离
的距离

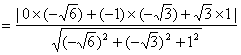
![]() .
.


科目:高中数学 来源:南昌模拟 题型:单选题
| A.{a|a>1} | B.{a|0<a<
| ||||
C.{a|0<a<
| D.{a|a0<a<
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.(-∞,1) | B.(-∞,2) | C.(-∞,1] | D.(-∞,2] |
查看答案和解析>>
科目:高中数学 来源:丰台区二模 题型:单选题
| A.是偶函数,且在(-∞,+∞)上是减函数 |
| B.是偶函数,且在(-∞,+∞)上是增函数 |
| C.是奇函数,且在(-∞,+∞)上是减函数 |
| D.是奇函数,且在(-∞,+∞)上是增函数 |
查看答案和解析>>
科目:高中数学 来源:东城区模拟 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com