已知集合A={a1,a2…an}(0≤a1<a2<…<an,n∈N*,n≥3)具有性质P:对任意i,j(1≤i≤j≤n),ai+aj与aj-ai至少一个属于A,
(1)分别判断集合M={0,2,4}与N=(1,2,3)是否具有性质P,并说明理由;
(2)①求证:0∈A;②当n=3时,集合A中元素a1、a2、a3是否一定成等差数列,若是,请证明;若不是,请说明理由;
(3)对于集合A中元素a1、a2、…an,若an=2012,求数列{an}的前n项和Sn(用n表示).
【答案】
分析:(1)根据题意分别把集合M和N中的元素代入:a
i+a
j与a
j-a
i进行验证,可判断是否具有性质P;
(2)①根据a
1、a
2、…a
n的大小关系和性质P,可得a
n+a
n=2a
n>a
n,则a
n-a
n=0=a
1∈A,
②由a
1、a
2、a
3的大小关系和由性质P判断出:a
1=a
3-a
3=0∈A,a
3-a
2=a
2,即得2a
2=a
1+a
3,故结论得证;
(3)由a
1、a
2、…a
n的关系和性质P,可求出元素a
1、a
2、…a
n的表达式,再代入所求的前n项和S
n进行化简得
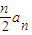
,代入a
n=2012求出S
n.
解答:解:(1)由题意得,
对于集合M:得2-0=2,4-2=2,4-0=4,0-0=2-2=4-4=0,
∵2,4,0∈M,∴集合具有性质P.
对于集合N:得2+2=4,2-2=0,
∵4,0∉N,∴集合N不具性质P,
(2)证明:①∵0≤a
1<a
2<…<a
n,n∈N
*,n≥3,
∴a
n+a
n=2a
n>a
n,则a
n-a
n=0=a
1∈A,
②当n=3时,集合A中元素a
1,a
2,a
3一定成等差数列.
证明:当n=3时,0≤a
1<a
2<a
3,
∴0≤a
3-a
3<a
3-a
2<a
3-a
1,
且a
3+a
3>a
3,∴a
3+a
3∉A,∴a
3-a
3=0∈A,∴a
1=0∈A,
则a
3+a
2>a
3,∴a
3+a
2∉A,∴a
3-a
2∈A,
∴a
3-a
2=a
2,即a
3=2a
2,又∵a
1=0,∴2a
2=a
1+a
3,
故a
1,a
2,a
3成等差数列,
(3)由题意得,0≤a
1<a
2<…<a
n,∴0≤a
n-a
n<a
n-a
n-1<…<a
n-a
1,
∴a
n+a
n-i>a
n(i=1,2,…n-1),∴a
n-a
n-i∈A,
∴a
1=a
n-a
n,a
2=a
n-a
n-1,a
3=a
n-a
n-2,…a
n=a
n-a
1,
∴S
n=a
1+a
2+…+a
n=na
n-(a
1+a
2+…+a
n),即S
n=na
n-S
n,
则S
n=
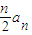
=
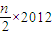
=606n.
点评:本题考查了等差数列的证明,数列求和等综合问题,以及新定义的灵活应用能力,难度较大.

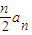 ,代入an=2012求出Sn.
,代入an=2012求出Sn.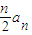 =
=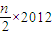 =606n.
=606n.
