已知三角形三个顶点为O(0,0),A(1,1),B(2,4).
(1)求△AOB外接圆的方程,并写出圆心坐标和半径;
(2)求△AOB的面积.
【答案】
分析:(1)设出圆的标准方程,列出方程组,求出圆心坐标,求出半径,即可得到△AOB外接圆的方程;
(2)写出OA的直线方程,求出B到直线的距离,求出OA的长度,即可求解△AOB的面积.
解答:解:(1)设所求圆的方程为:(x+a)
2+(y+b)
2=r
2,
因为O(0,0),A(1,1),B(2,4)在圆上,
所以
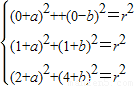
,
解得:
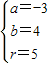
,
所求圆的标准方程为:(x+3)
2+(y-4)
2=25 圆心:(-3,4),半径为5
(2)由题意直线OA的距离为:
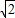
,
OA的方程为:x-y=0,点B到直线x-y=0的距离为:

=
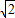
,
所以所求三角形的面积为:
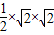
=1.
点评:本题考查圆的标准方程的求法,三角形的面积的求法,考查计算能力.

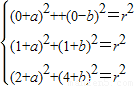 ,
,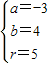 ,
, ,
, =
=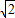 ,
,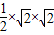 =1.
=1.
