Question

（本小题满分13分）某企业的产品以往专销欧美市场，在全球金融风暴的影响下，欧美市场的销量受到严重影响，该企业在政府的大力扶助下积极开拓国内市场，并基本形成了市场规模；自2009年9月以来的第n个月（2009年9月为第一个月）产品的内销量、出口量和销售总量（销售总量=内销量与出口量的和）分别为bn、cn和an(单位：万件)，依据销售统计数据发现形成如下营销趋势：bn + 1 = a an，cn + 1 = an + b an2 （其中a、b为常数），已知a1 = 1万件，a2 = 1.5万件，a3 = 1.875万件．

    （1）求a，b的值，并写出an + 1与an满足的关系式；

    （2）试用你所学的数学知识论证销售总量逐月递增且控制在2万件内；

    （3）试求从2009年9月份以来的第n个月的销售总量an关于n的表达式．

 

Answer 1

【答案】

（1）an + 1 = 2a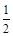n –an2 (n∈N*)

（2）略（3）an = 2 – 2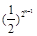

【解析】（1）依题意：an + 1 = bn + 1 + cn + 1 = a an + an + b an2，

则a2 = a a1 + a1 + b a12    ∴a + 1 + b = 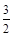           ①

则a3 = a a2 + a2 + b a2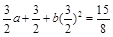2   ∴        ②

解①②得a = 1，b = –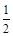  从而an + 1 = 2an –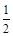an2 (n∈N*)     ………………………5分[来

（2）证法（Ⅰ）由于an + 1 = 2an –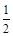an2 = –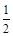 (an – 2)2 + 2≤2．         

但an + 1≠2，否则可推得a 1= a 2= 2与a 1= 1，a2 = 1.5矛盾．故an + 1＜2  于是an＜2

又an + 1– an= –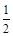an2 + 2an – an = –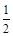an (an – 2) ＞0，

所以an + 1＞an 从而an＜an + 1＜2               …………………………………9分

证法（Ⅱ）由数学归纳法

（i）当n = 1时，a1 = 1，a2 = 1.5，显然a1＜a2＜2成立

（ii）假设n = k时，  ak＜ak + 1＜2成立．

由于函数f (x) = –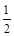x2 + 2x = –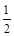(x – 2)2 + 2在[0，2]上为增函数，

则f (ak) ＜f (ak + 1) ＜f (2)即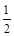ak (4 – ak) 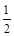＜ak + 1(4 –ak + 1) 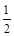＜×2×(4 – 2)

 即 ak + 1＜ak + 2＜2成立． 综上可得n∈N*有an＜an + 1＜2 …………………………9分

（3）由an + 1 = 2an –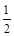an2得2 (an + 1– 2) = – (an – 2)2  即(2 – an + 1) = 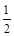(2 – an)2

又由（2）an＜an + 1＜2可知2 – an + 1＞0，2 – an＞0  

则lg (2 – an + 1) = 2 lg (2 – an) – lg 2   ∴lg (2 – an +1) – lg2 = 2[lg (2 – an) – lg2]

即{lg (2 – an + 1) – lg2}为等比数列，公比为2，首项为lg (2 – a1) – lg 2 = –lg 2

故lg (2 – an) – lg 2 = (–lg 2)·2n – 1 ∴an = 2 – 2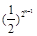 (n∈N*)为所求………13分