
已知,椭圆C以过点A(1,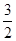 ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。
求椭圆C的方程;
E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
(1)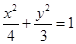 .(2)直线EF的斜率为定值,其值为
.(2)直线EF的斜率为定值,其值为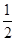 。
。
【解析】
试题分析:(1)由题意,c=1,可设椭圆方程为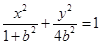 。
。
因为A在椭圆上,所以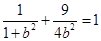 ,解得
,解得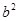 =3,
=3,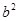 =
=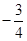 (舍去)。
(舍去)。
所以椭圆方程为 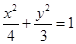 . 6分
. 6分
(2)设直线AE方程:得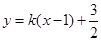 ,代入
,代入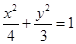 得
得
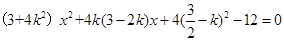
设E(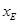 ,
,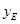 ),F(
),F(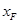 ,
, ).因为点A(1,
).因为点A(1,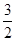 )在椭圆上,所以
)在椭圆上,所以
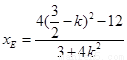 ,
,
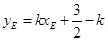 。 9分
。 9分
又直线AF的斜率与AE的斜率互为相反数,在上式中以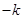 代
代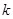 ,可得
,可得
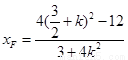 ,
,
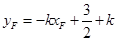 。
。
所以直线EF的斜率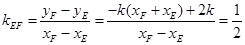 。
。
即直线EF的斜率为定值,其值为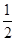 。
13分
。
13分
考点:本题主要考查椭圆的标准方程及其几何性质,直线与椭圆的位置关系。
点评:中档题,本题求椭圆的标准方程,主要运用的椭圆的几何性质,注意明确焦点轴和a,b,c的关系。研究直线与圆锥曲线的位置关系,往往应用韦达定理,通过“整体代换”,简化解题过程,实现解题目的。


科目:高中数学 来源: 题型:
已知,椭圆C以过点A(1,![]() ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。
(Ⅰ)求椭圆C的方程;
(Ⅱ)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。 ![]()
![]()
查看答案和解析>>
科目:高中数学 来源:2014届安徽省高二下第三次(期末)质检文科数学卷(解析版) 题型:解答题
已知,椭圆C以过点A(1,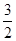 ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。
(1)求椭圆C的方程;
(2)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
查看答案和解析>>
科目:高中数学 来源:2013届河北省高二下学期第一次考试文科数学试卷 题型:解答题
已知,椭圆C以过点A(1,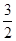 ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。
(1)求椭圆C的方程;
(2)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
查看答案和解析>>
科目:高中数学 来源:2013届山东省济宁市高二3月月考文科数学试卷 题型:解答题
已知,椭圆C以过点A(1,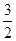 ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。
(1)求椭圆C的方程;
(2)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com