
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若存在![]() ,且
,且![]() ,使得
,使得![]() ,求证:
,求证: ![]() .
.
【答案】(1)单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)求函数的单调区间,转化为求函数导数值大于零或小于零的不等式的解;(2)根据题意对![]() 进行分类讨论,当
进行分类讨论,当![]() 时显然不行,
时显然不行, ![]() 时,不能有
时,不能有![]() ,设
,设![]() ,则由
,则由![]() 即可,利用单调性即可证出.
即可,利用单调性即可证出.
试题解析:(1)当![]() 时,
时, ![]() ,
,
又![]() ,由
,由![]() ,
,
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)由![]() ,当
,当![]() 时,
时, ![]() ,此时
,此时![]() 在R上单调递增;
在R上单调递增;
由![]() 可得
可得![]() ,与
,与![]() 相矛盾,
相矛盾,
所以![]() ,且
,且![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
若![]() ,则由
,则由![]() 可得
可得![]() ,与
,与![]() 相矛盾,
相矛盾,
同样不能有![]() ,
,
不妨设![]() ,则由
,则由![]() ,
,
因为![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,且
上单调递增,且![]() ,
,
所以当![]() 时,
时, ![]() .
.
由![]() ,
, ![]() ,可得
,可得![]() ,故
,故![]() ,
,
又![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,所以
,所以![]() ,
,
所以![]() ,同理
,同理![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】某车间20名工人年龄数据如下表:
年龄(岁) | 工人数(人) |
19 | 1 |
28 | 3 |
29 | 3 |
30 | 5 |
31 | 4 |
32 | 3 |
40 | 1 |
合计 | 20 |
(1)求这20名工人年龄的众数与极差;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)求这20名工人年龄的方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点A(x , y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间t=0时,点A的坐标是( ![]() ,
, ![]() ),则当0≤t≤12时,动点A的纵坐标y关于 t(单位:秒)的函数的单调递增区间是 .
),则当0≤t≤12时,动点A的纵坐标y关于 t(单位:秒)的函数的单调递增区间是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:函数f(x)=lg(ax2﹣x+ ![]() a)定义域为R;命题q:不等式3x﹣9x<a对任意x∈R恒成立.
a)定义域为R;命题q:不等式3x﹣9x<a对任意x∈R恒成立.
(1)如果p是真命题,求实数a的取值范围;
(2)如果命题“p或q”为真命题且“p且q”为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(x+1),g(x)=log2(3x+1).
(1)求出使g(x)≥f(x)成立的x的取值范围;
(2)当x∈[0,+∞)时,求函数y=g(x)﹣f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,底面ABCD为直角梯形,∠BAD=90°,AD∥BC,AB=BC=2,AD=4,PA⊥底面ABCD,PD与底面ABCD成30°角,E是PD的中点. 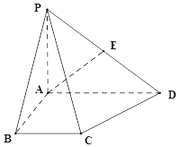
(1)点H在AC上且EH⊥AC,求 ![]() 的坐标;
的坐标;
(2)求AE与平面PCD所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角ABC中,角A、B、C所对的边分别为a,b,c,b=4,c=6,且asinB=2![]() .
.
(1)求角A的大小;
(2)若D为BC的中点,求线段AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知2件次品和a件正品放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出a件正品时检测结束,已知前两次检测都没有检测出次品的概率为![]() .
.
(1) 求实数a的值;
(2) 若每检测一件产品需要费用100元,设X表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com