
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| n |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省巴蜀中学高一(下)期中数学试卷(理科)(解析版) 题型:选择题
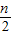 );若n是奇数,则将它乘3加1(即3n+1).不断重复这样的运算,经过有限步后,一定可以得到1”.如6→3→10→5→16→8→4→2→1,如果对正整数n(首项),按上述规则实施变换(注:1可以多次出现)后的第八项为1,那么n的所有可能值共有( )
);若n是奇数,则将它乘3加1(即3n+1).不断重复这样的运算,经过有限步后,一定可以得到1”.如6→3→10→5→16→8→4→2→1,如果对正整数n(首项),按上述规则实施变换(注:1可以多次出现)后的第八项为1,那么n的所有可能值共有( )查看答案和解析>>
科目:高中数学 来源: 题型:
1-4=-(1+2),
1-4+9=1+2+3,
1-4+9-16=-(1+2+3+4),
1-4+9-16+25=1+2+3+4+5的第n个式子为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
1-4=-(1+2),
1-4+9=1+2+3,
1-4+9-16=-(1+2+3+4),
1-4+9-16+25=1+2+3+4+5的第n个式子为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com