Question

由原点O向曲线f(x)=x³-3ax²+x(a≠0)引切线,切点P₁(x₁,y₁)异于O,再由点P₁引此曲线的切线,切点P₂(x₂,y₂)异于P₁,如此继续下去,得到点列{P_n(x_n,y_n)}.

(1)求x₁;

(2)求证:数列{x_n-a}为等比数列;

(3)令b_n=n|x_n-a|,T_n为数列{b_n}的前n项的和,若T_n＞2对n∈N^*恒成立,求a的取值范围.

Answer 1

(1)解:f′(x)=3x²-6ax+1,

过切点P₁(x₁,y₁)的切线方程为y-y₁=(3x₁²-6ax₁+1)(x-x₁),

由于切线过原点O,因此0-(x₁³-3ax₁²+x₁)=(3x₁²-6ax₁+1)(0-x₁).

解得x₁=a.

(2)证明:过切点P_n+1(x_n+1,y_n+1)的切线方程为y-y_n+1=(3x_n+1²-6ax_n+1+1)(x-x_n+1),

由于切线过点P_n(x_n,y_n),因此y_n-y_n+1=(3x_n+1²-6ax_n+1+1)(x_n-x_n+1).

化简得x_n+2x_n+1=3a,

∴x_n-a=-2(x_n+1-a),

即=-.

∴数列{x_n-a}是以x₁-a=为首项,公比为-的等比数列.

(3)解:由(2)得x_n-a=(-)^n-1,

b_n=|a|,

T_n=|a|(+++…+).

令S_n=+++…+,

由错位相减可求得S_n=2［］,

∴T_n=2|a|()＞2.

由单调性得≤＜1.

∴1＜≤4,|a|＞.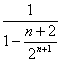

要使T_n＞2对n∈N^*恒成立,故|a|＞4.

∴a的取值范围是(-∞,-4)∪(4,+∞).