
分析 (Ⅰ)直线PA:y-y0=kPA(x-x0),代入抛物线方程,得出$△=0⇒k_{PA}^2-2{x_0}{k_{PA}}+2{y_0}=0$,同理,有$k_{PB}^2-2{x_0}{k_{PB}}+2{y_0}=0$,kPA,kPB分别为方程:k2-2x0k+2y0=0的两个不同的实数根,利用韦达定理求点P的轨迹方程;
(Ⅱ)求出直线AB的方程,即可得出结论.
解答 解:(Ⅰ)设P(x0,y0),则直线PA:y-y0=kPA(x-x0),代入抛物线方程:x2-2kPAx-2y0+2kPAx0=0,
因为直线与抛物线相切,所以$△=0⇒k_{PA}^2-2{x_0}{k_{PA}}+2{y_0}=0$,…(2分)
同理,有$k_{PB}^2-2{x_0}{k_{PB}}+2{y_0}=0$,…(3分)
所以kPA,kPB分别为方程:k2-2x0k+2y0=0的两个不同的实数根,…(5分)
kPAkPB=-2=2y0,所以y0=-1,所以点P的轨迹方程为y=-1.…(6分)
(Ⅱ)设A(x1,y1),B(x2,y2),
由$y=\frac{1}{2}{x^2}$,y'=x,所以抛物线在A,B点的切线方程分别为x1x-y-y1=0,x2x-y-y2=0,…(8分)
又都过点P(x0,-1),所以$\left\{\begin{array}{l}{x_1}{x_0}-{y_1}+1=0\\{x_2}{x_0}-{y_2}+1=0\end{array}\right.$…(9分)
所以直线AB的方程为xx0-y+1=0,…(11分)
所以直线AB恒过定点(0,1).…(12分)
点评 本题考查直线与抛物线的位置关系,圆锥曲线方程的综合应用,函数的导数以及切线方程的应用,难度比较大的压轴题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1-a}{2}$ | B. | $\frac{a}{2}$ | C. | 1-a | D. | $\frac{1+a}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
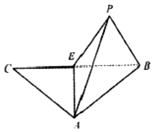 等腰△ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使二面角P-AE-C的大小为120°,设点P在面ABE上的射影为H.
等腰△ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使二面角P-AE-C的大小为120°,设点P在面ABE上的射影为H.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com